Question Number 111175 by 9696147350 last updated on 02/Sep/20
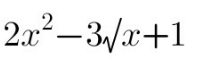
Answered by ajfour last updated on 02/Sep/20
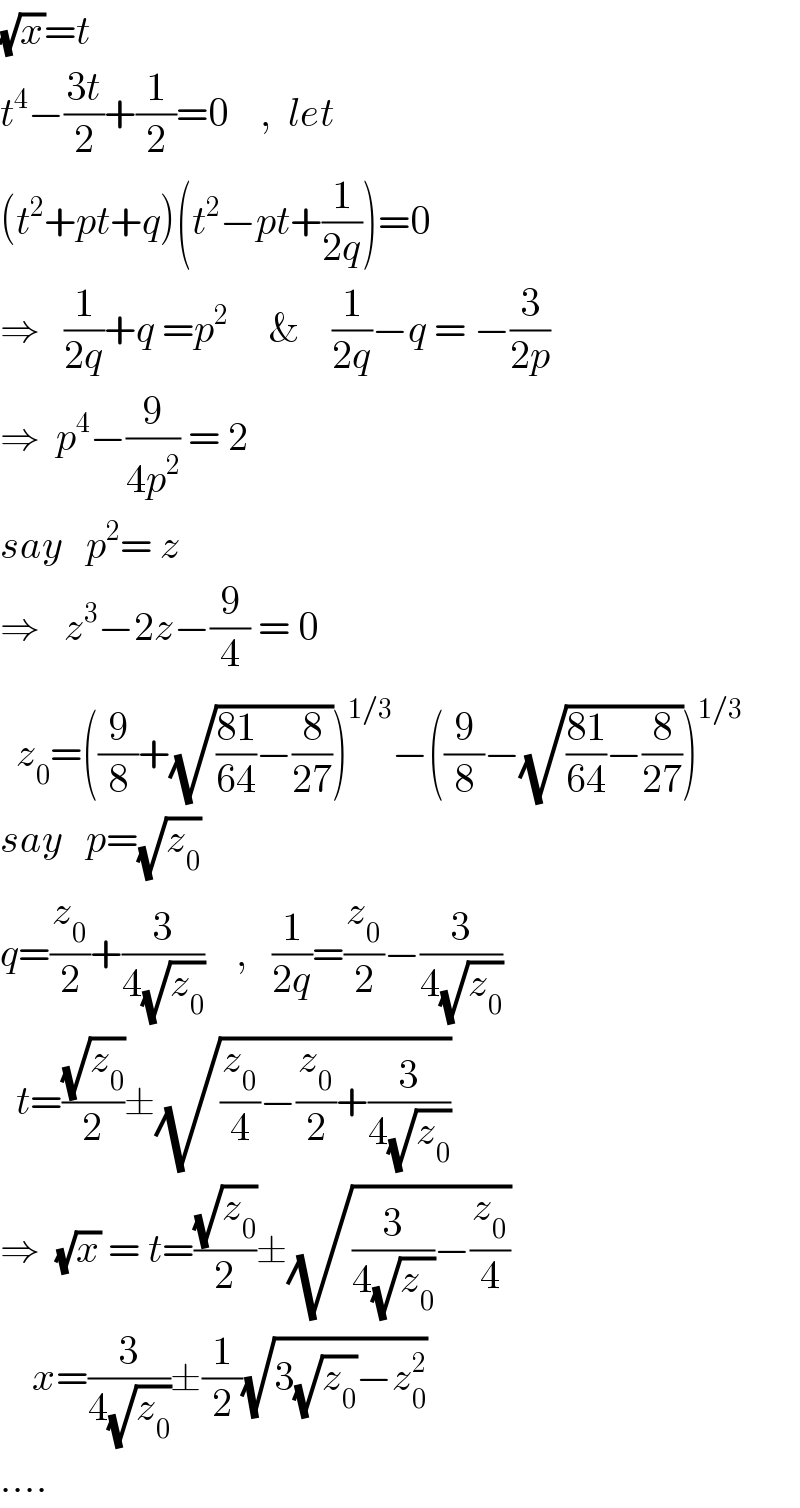
$$\sqrt{{x}}={t} \\ $$$${t}^{\mathrm{4}} −\frac{\mathrm{3}{t}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0}\:\:\:\:,\:\:{let} \\ $$$$\left({t}^{\mathrm{2}} +{pt}+{q}\right)\left({t}^{\mathrm{2}} −{pt}+\frac{\mathrm{1}}{\mathrm{2}{q}}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\frac{\mathrm{1}}{\mathrm{2}{q}}+{q}\:={p}^{\mathrm{2}} \:\:\:\:\:\&\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}{q}}−{q}\:=\:−\frac{\mathrm{3}}{\mathrm{2}{p}} \\ $$$$\Rightarrow\:\:{p}^{\mathrm{4}} −\frac{\mathrm{9}}{\mathrm{4}{p}^{\mathrm{2}} }\:=\:\mathrm{2} \\ $$$${say}\:\:\:{p}^{\mathrm{2}} =\:{z} \\ $$$$\Rightarrow\:\:\:{z}^{\mathrm{3}} −\mathrm{2}{z}−\frac{\mathrm{9}}{\mathrm{4}}\:=\:\mathrm{0} \\ $$$$\:\:{z}_{\mathrm{0}} =\left(\frac{\mathrm{9}}{\mathrm{8}}+\sqrt{\frac{\mathrm{81}}{\mathrm{64}}−\frac{\mathrm{8}}{\mathrm{27}}}\right)^{\mathrm{1}/\mathrm{3}} −\left(\frac{\mathrm{9}}{\mathrm{8}}−\sqrt{\frac{\mathrm{81}}{\mathrm{64}}−\frac{\mathrm{8}}{\mathrm{27}}}\right)^{\mathrm{1}/\mathrm{3}} \\ $$$${say}\:\:\:{p}=\sqrt{{z}_{\mathrm{0}} } \\ $$$${q}=\frac{{z}_{\mathrm{0}} }{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}\sqrt{{z}_{\mathrm{0}} }}\:\:\:\:,\:\:\:\frac{\mathrm{1}}{\mathrm{2}{q}}=\frac{{z}_{\mathrm{0}} }{\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{4}\sqrt{{z}_{\mathrm{0}} }} \\ $$$$\:\:{t}=\frac{\sqrt{{z}_{\mathrm{0}} }}{\mathrm{2}}\pm\sqrt{\frac{{z}_{\mathrm{0}} }{\mathrm{4}}−\frac{{z}_{\mathrm{0}} }{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}\sqrt{{z}_{\mathrm{0}} }}} \\ $$$$\Rightarrow\:\:\sqrt{{x}}\:=\:{t}=\frac{\sqrt{{z}_{\mathrm{0}} }}{\mathrm{2}}\pm\sqrt{\frac{\mathrm{3}}{\mathrm{4}\sqrt{{z}_{\mathrm{0}} }}−\frac{{z}_{\mathrm{0}} }{\mathrm{4}}} \\ $$$$\:\:\:\:{x}=\frac{\mathrm{3}}{\mathrm{4}\sqrt{{z}_{\mathrm{0}} }}\pm\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{3}\sqrt{{z}_{\mathrm{0}} }−{z}_{\mathrm{0}} ^{\mathrm{2}} } \\ $$$$…. \\ $$
