Question Number 111187 by ajfour last updated on 02/Sep/20
Commented by ajfour last updated on 03/Sep/20
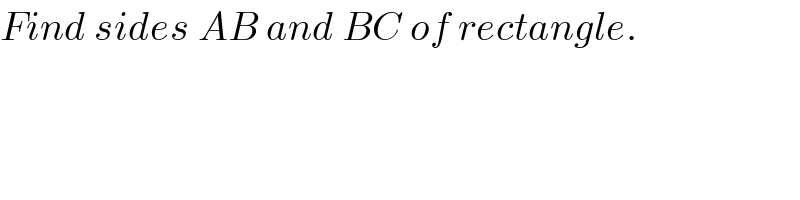
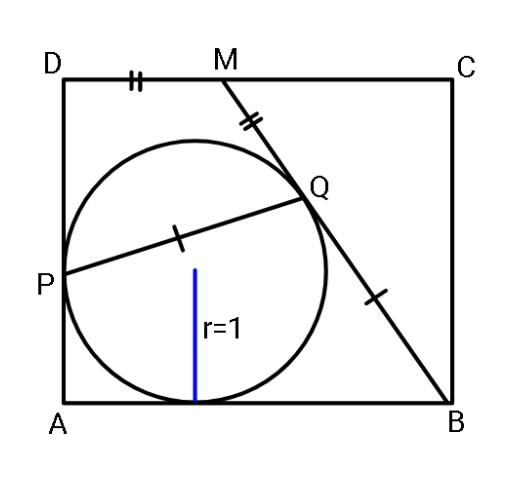
$${Find}\:{sides}\:{AB}\:{and}\:{BC}\:{of}\:{rectangle}.\:\:\: \\ $$
Answered by ajfour last updated on 03/Sep/20
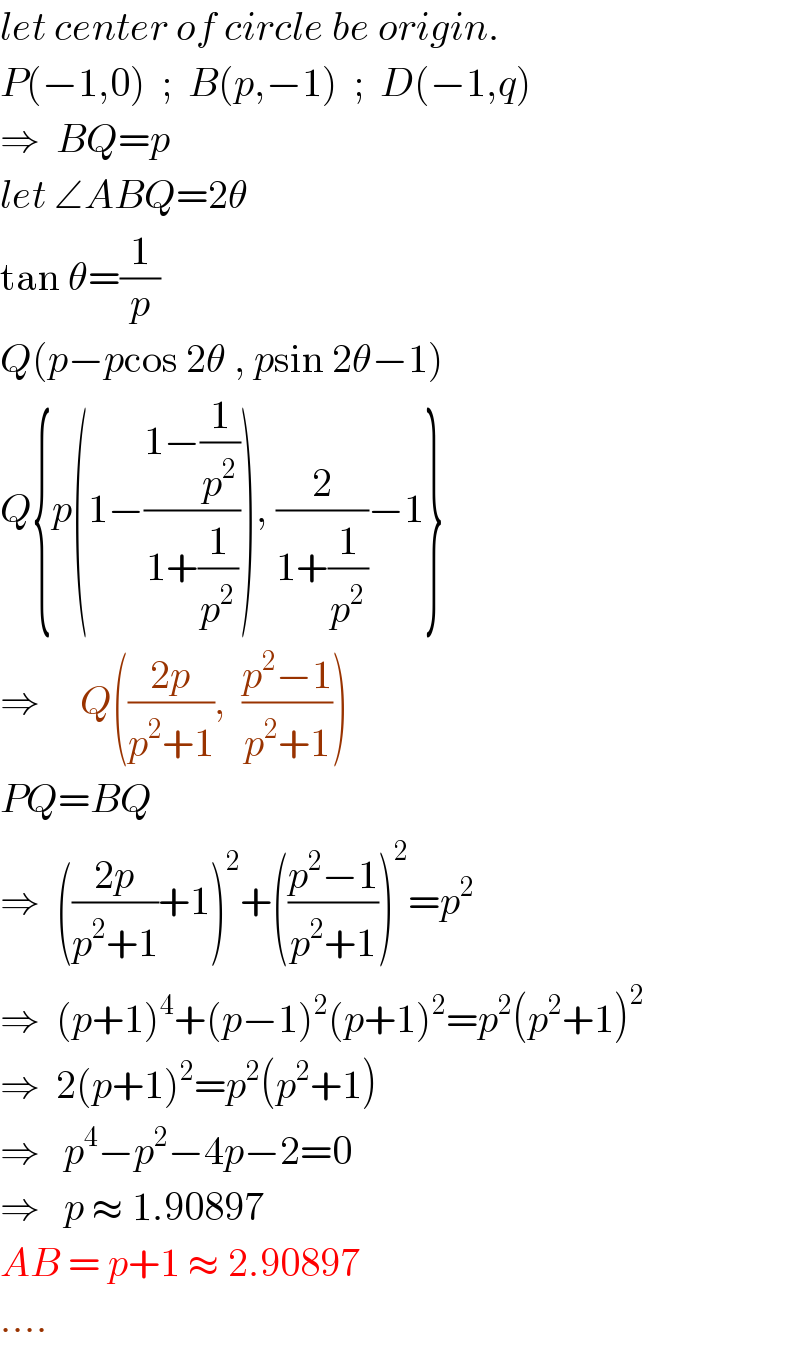
$${let}\:{center}\:{of}\:{circle}\:{be}\:{origin}. \\ $$$${P}\left(−\mathrm{1},\mathrm{0}\right)\:\:;\:\:{B}\left({p},−\mathrm{1}\right)\:\:;\:\:{D}\left(−\mathrm{1},{q}\right) \\ $$$$\Rightarrow\:\:{BQ}={p} \\ $$$${let}\:\angle{ABQ}=\mathrm{2}\theta \\ $$$$\mathrm{tan}\:\theta=\frac{\mathrm{1}}{{p}} \\ $$$${Q}\left({p}−{p}\mathrm{cos}\:\mathrm{2}\theta\:,\:{p}\mathrm{sin}\:\mathrm{2}\theta−\mathrm{1}\right) \\ $$$${Q}\left\{{p}\left(\mathrm{1}−\frac{\mathrm{1}−\frac{\mathrm{1}}{{p}^{\mathrm{2}} }}{\mathrm{1}+\frac{\mathrm{1}}{{p}^{\mathrm{2}} }}\right),\:\frac{\mathrm{2}}{\mathrm{1}+\frac{\mathrm{1}}{{p}^{\mathrm{2}} }}−\mathrm{1}\right\} \\ $$$$\Rightarrow\:\:\:\:\:{Q}\left(\frac{\mathrm{2}{p}}{{p}^{\mathrm{2}} +\mathrm{1}},\:\:\frac{{p}^{\mathrm{2}} −\mathrm{1}}{{p}^{\mathrm{2}} +\mathrm{1}}\right) \\ $$$${PQ}={BQ} \\ $$$$\Rightarrow\:\:\left(\frac{\mathrm{2}{p}}{{p}^{\mathrm{2}} +\mathrm{1}}+\mathrm{1}\right)^{\mathrm{2}} +\left(\frac{{p}^{\mathrm{2}} −\mathrm{1}}{{p}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} ={p}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\left({p}+\mathrm{1}\right)^{\mathrm{4}} +\left({p}−\mathrm{1}\right)^{\mathrm{2}} \left({p}+\mathrm{1}\right)^{\mathrm{2}} ={p}^{\mathrm{2}} \left({p}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{2}\left({p}+\mathrm{1}\right)^{\mathrm{2}} ={p}^{\mathrm{2}} \left({p}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\Rightarrow\:\:\:{p}^{\mathrm{4}} −{p}^{\mathrm{2}} −\mathrm{4}{p}−\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:{p}\:\approx\:\mathrm{1}.\mathrm{90897} \\ $$$${AB}\:=\:{p}+\mathrm{1}\:\approx\:\mathrm{2}.\mathrm{90897} \\ $$$$…. \\ $$
