Question Number 111213 by mnjuly1970 last updated on 02/Sep/20
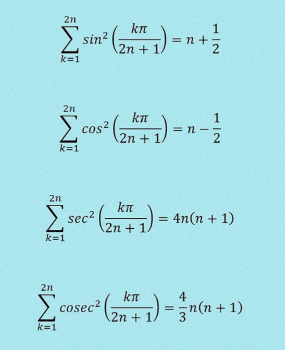
Answered by mathmax by abdo last updated on 02/Sep/20
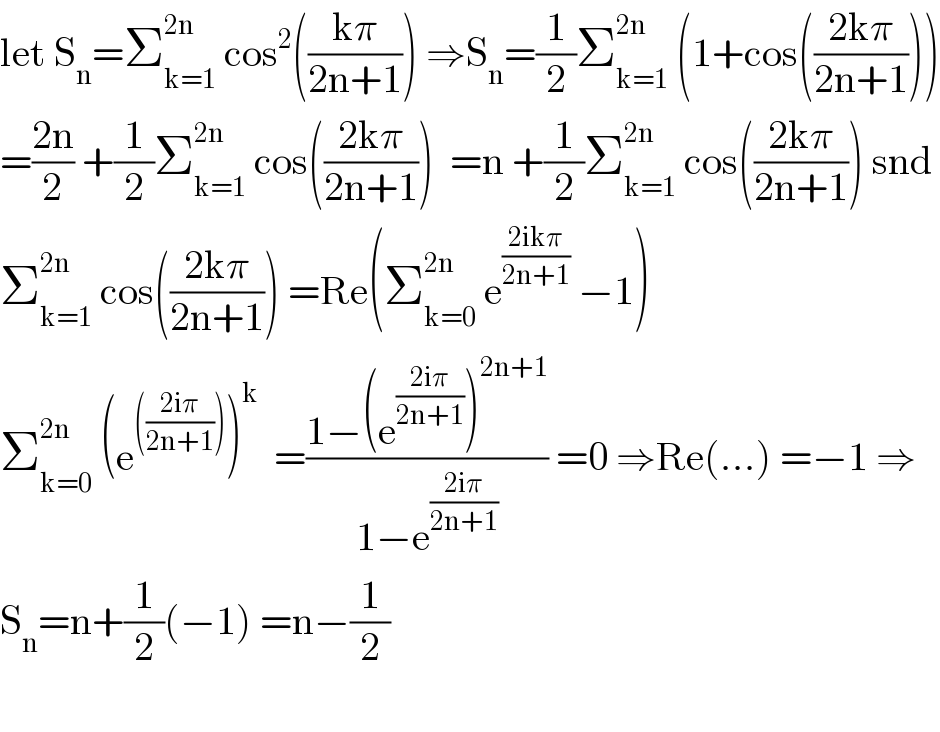
$$\mathrm{let}\:\mathrm{S}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{2n}} \:\mathrm{cos}^{\mathrm{2}} \left(\frac{\mathrm{k}\pi}{\mathrm{2n}+\mathrm{1}}\right)\:\Rightarrow\mathrm{S}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{2n}} \:\left(\mathrm{1}+\mathrm{cos}\left(\frac{\mathrm{2k}\pi}{\mathrm{2n}+\mathrm{1}}\right)\right) \\ $$$$=\frac{\mathrm{2n}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{2n}} \:\mathrm{cos}\left(\frac{\mathrm{2k}\pi}{\mathrm{2n}+\mathrm{1}}\right)\:\:=\mathrm{n}\:+\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{2n}} \:\mathrm{cos}\left(\frac{\mathrm{2k}\pi}{\mathrm{2n}+\mathrm{1}}\right)\:\mathrm{snd} \\ $$$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{2n}} \:\mathrm{cos}\left(\frac{\mathrm{2k}\pi}{\mathrm{2n}+\mathrm{1}}\right)\:=\mathrm{Re}\left(\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}} \:\mathrm{e}^{\frac{\mathrm{2ik}\pi}{\mathrm{2n}+\mathrm{1}}} \:−\mathrm{1}\right) \\ $$$$\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}} \:\left(\mathrm{e}^{\left(\frac{\mathrm{2i}\pi}{\mathrm{2n}+\mathrm{1}}\right)} \right)^{\mathrm{k}} \:\:=\frac{\mathrm{1}−\left(\mathrm{e}^{\frac{\mathrm{2i}\pi}{\mathrm{2n}+\mathrm{1}}} \right)^{\mathrm{2n}+\mathrm{1}} }{\mathrm{1}−\mathrm{e}^{\frac{\mathrm{2i}\pi}{\mathrm{2n}+\mathrm{1}}} }\:=\mathrm{0}\:\Rightarrow\mathrm{Re}\left(…\right)\:=−\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{S}_{\mathrm{n}} =\mathrm{n}+\frac{\mathrm{1}}{\mathrm{2}}\left(−\mathrm{1}\right)\:=\mathrm{n}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 03/Sep/20
$${thank}\:{you}\:{very}\:{much}\:{sir}… \\ $$
Answered by mathmax by abdo last updated on 02/Sep/20
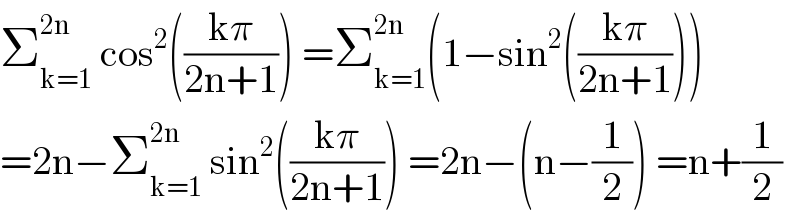
$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{2n}} \:\mathrm{cos}^{\mathrm{2}} \left(\frac{\mathrm{k}\pi}{\mathrm{2n}+\mathrm{1}}\right)\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{2n}} \left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \left(\frac{\mathrm{k}\pi}{\mathrm{2n}+\mathrm{1}}\right)\right) \\ $$$$=\mathrm{2n}−\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{2n}} \:\mathrm{sin}^{\mathrm{2}} \left(\frac{\mathrm{k}\pi}{\mathrm{2n}+\mathrm{1}}\right)\:=\mathrm{2n}−\left(\mathrm{n}−\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\mathrm{n}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$
