Question-111235

Question Number 111235 by aurpeyz last updated on 02/Sep/20

Commented by aurpeyz last updated on 02/Sep/20

Pls explain why T_1 is negative in equation 1 but Positive in equation 2. i just want to understand that scenerio. pls

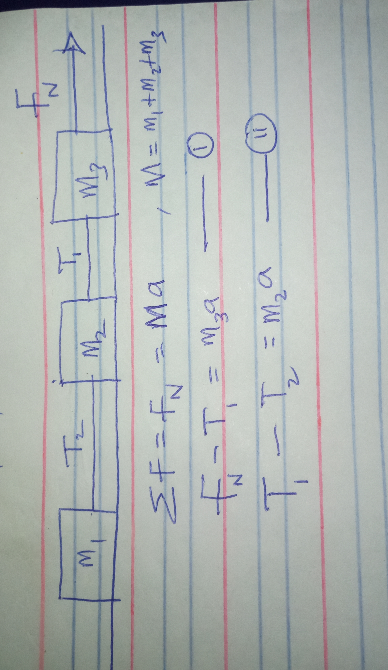
$$\mathrm{Pls}\:\mathrm{explain}\:\mathrm{why}\:\mathrm{T}_{\mathrm{1}} \:\mathrm{is}\:\mathrm{negative}\:\mathrm{in}\:\mathrm{equation}\:\mathrm{1} \\ $$$$\mathrm{but}\:\mathrm{Positive}\:\mathrm{in}\:\mathrm{equation}\:\mathrm{2}. \\ $$$${i}\:{just}\:{want}\:{to}\:{understand}\:{that}\:{scenerio}.\:{pls} \\ $$

Answered by Rio Michael last updated on 02/Sep/20

This is by your assumption, that if a force has a direction to the right relative to another force, it is positive. This is how the whole system works. The force F_N is applied on m_1 which is connected to m_2 by a string (of negligible mass). This string consequently gets tensioned T_(1.) when looking at the m_1 mass, the F_N force is to the right, while the T_1 force is to the left(trying to slow down m_1 ) so by your assumption that forces to the right are positive F_N −T_1 = m_1 a (Newtons law). Now examining m_2 with forces T_1 and T_2 acting, we noticed that T_1 tries to acceleratd m_2 while T_2 tries to slow it down ⇒ T_1 −T_2 = m_2 a

$$\mathrm{This}\:\mathrm{is}\:\mathrm{by}\:\mathrm{your}\:\mathrm{assumption},\:\mathrm{that}\:\mathrm{if}\:\mathrm{a}\:\mathrm{force}\:\mathrm{has}\:\mathrm{a}\:\mathrm{direction}\:\mathrm{to}\:\mathrm{the} \\ $$$$\mathrm{right}\:\mathrm{relative}\:\mathrm{to}\:\mathrm{another}\:\mathrm{force},\:\mathrm{it}\:\mathrm{is}\:\mathrm{positive}. \\ $$$$\mathrm{This}\:\mathrm{is}\:\mathrm{how}\:\mathrm{the}\:\mathrm{whole}\:\mathrm{system}\:\mathrm{works}.\: \\ $$$$\:\:\:\mathrm{The}\:\mathrm{force}\:{F}_{{N}} \:\mathrm{is}\:\mathrm{applied}\:\mathrm{on}\:{m}_{\mathrm{1}} \:\mathrm{which}\:\mathrm{is}\:\mathrm{connected}\:\mathrm{to}\:{m}_{\mathrm{2}} \:\mathrm{by} \\ $$$$\mathrm{a}\:\mathrm{string}\:\left(\mathrm{of}\:\mathrm{negligible}\:\mathrm{mass}\right).\:\mathrm{This}\:\mathrm{string}\:\mathrm{consequently}\:\mathrm{gets}\:\mathrm{tensioned}\:{T}_{\mathrm{1}.} \\ $$$$\mathrm{when}\:\mathrm{looking}\:\mathrm{at}\:\mathrm{the}\:{m}_{\mathrm{1}} \:\mathrm{mass},\:\mathrm{the}\:{F}_{{N}} \:\mathrm{force}\:\mathrm{is}\:\mathrm{to}\:\mathrm{the}\:\mathrm{right},\:\mathrm{while}\:\mathrm{the}\:{T}_{\mathrm{1}} \:\mathrm{force} \\ $$$$\mathrm{is}\:\mathrm{to}\:\mathrm{the}\:\mathrm{left}\left(\mathrm{trying}\:\mathrm{to}\:\mathrm{slow}\:\mathrm{down}\:{m}_{\mathrm{1}} \right)\:\mathrm{so}\:\mathrm{by}\:\mathrm{your}\:\mathrm{assumption}\:\mathrm{that}\: \\ $$$$\mathrm{forces}\:\mathrm{to}\:\mathrm{the}\:\mathrm{right}\:\mathrm{are}\:\mathrm{positive} \\ $$$$\:{F}_{{N}} −{T}_{\mathrm{1}} \:=\:{m}_{\mathrm{1}} \mathrm{a}\:\:\left({N}\mathrm{ewtons}\:\mathrm{law}\right). \\ $$$$\:\:\mathrm{Now}\:\mathrm{examining}\:{m}_{\mathrm{2}} \:\mathrm{with}\:\mathrm{forces}\:{T}_{\mathrm{1}} \:\mathrm{and}\:{T}_{\mathrm{2}} \:\mathrm{acting},\:\mathrm{we}\:\mathrm{noticed}\:\mathrm{that}\: \\ $$$${T}_{\mathrm{1}} \:\mathrm{tries}\:\mathrm{to}\:\mathrm{acceleratd}\:{m}_{\mathrm{2}} \:\mathrm{while}\:{T}_{\mathrm{2}} \:\mathrm{tries}\:\mathrm{to}\:\mathrm{slow}\:\mathrm{it}\:\mathrm{down} \\ $$$$\Rightarrow\:{T}_{\mathrm{1}} −{T}_{\mathrm{2}} \:=\:{m}_{\mathrm{2}} \mathrm{a} \\ $$

Commented by aurpeyz last updated on 03/Sep/20

$${thanks}\:{i}\:{now}\:{understsnd}\:{well}.\:{tension}\:{is}\:{a}\: \\ $$$${pulling}\:{force} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply