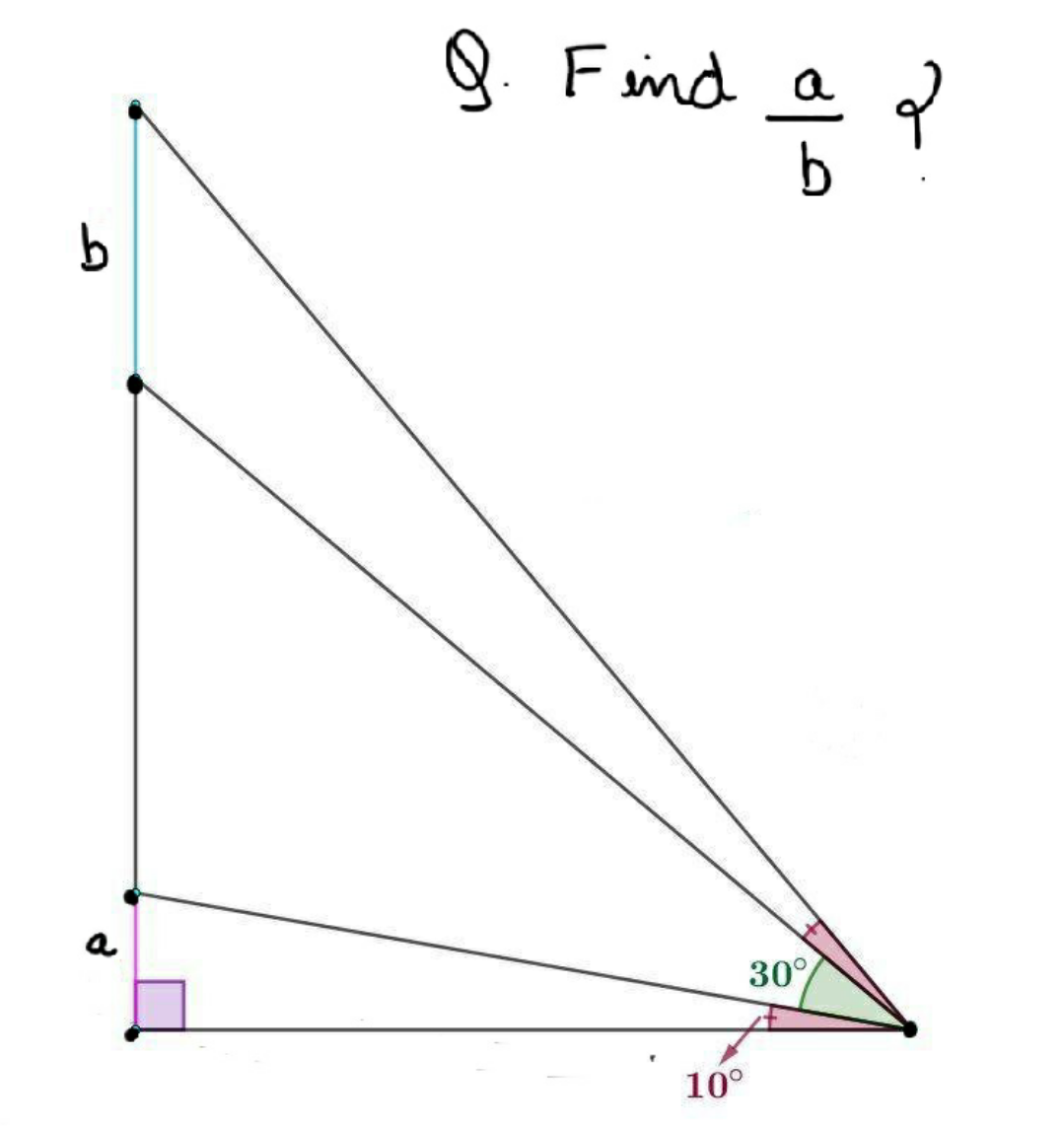
Question Number 111267 by I want to learn more last updated on 03/Sep/20
Answered by Her_Majesty last updated on 03/Sep/20
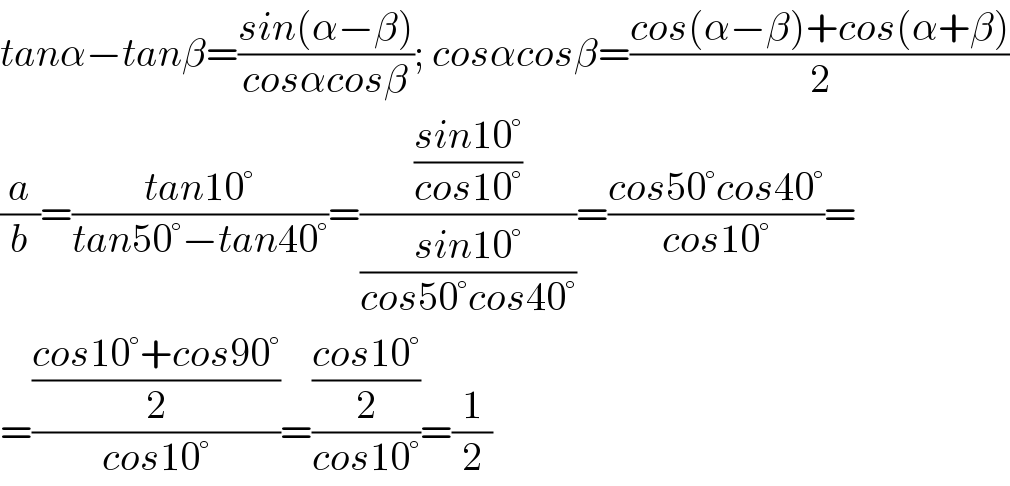
$${tan}\alpha−{tan}\beta=\frac{{sin}\left(\alpha−\beta\right)}{{cos}\alpha{cos}\beta};\:{cos}\alpha{cos}\beta=\frac{{cos}\left(\alpha−\beta\right)+{cos}\left(\alpha+\beta\right)}{\mathrm{2}} \\ $$$$\frac{{a}}{{b}}=\frac{{tan}\mathrm{10}°}{{tan}\mathrm{50}°−{tan}\mathrm{40}°}=\frac{\frac{{sin}\mathrm{10}°}{{cos}\mathrm{10}°}}{\frac{{sin}\mathrm{10}°}{{cos}\mathrm{50}°{cos}\mathrm{40}°}}=\frac{{cos}\mathrm{50}°{cos}\mathrm{40}°}{{cos}\mathrm{10}°}= \\ $$$$=\frac{\frac{{cos}\mathrm{10}°+{cos}\mathrm{90}°}{\mathrm{2}}}{{cos}\mathrm{10}°}=\frac{\frac{{cos}\mathrm{10}°}{\mathrm{2}}}{{cos}\mathrm{10}°}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by I want to learn more last updated on 03/Sep/20
$$\mathrm{Thanks}\:\mathrm{ma},\:\mathrm{i}\:\mathrm{appreciate} \\ $$
