Question Number 111382 by john santu last updated on 03/Sep/20
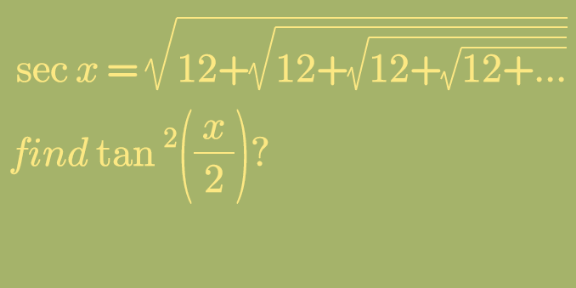
Commented by kaivan.ahmadi last updated on 03/Sep/20
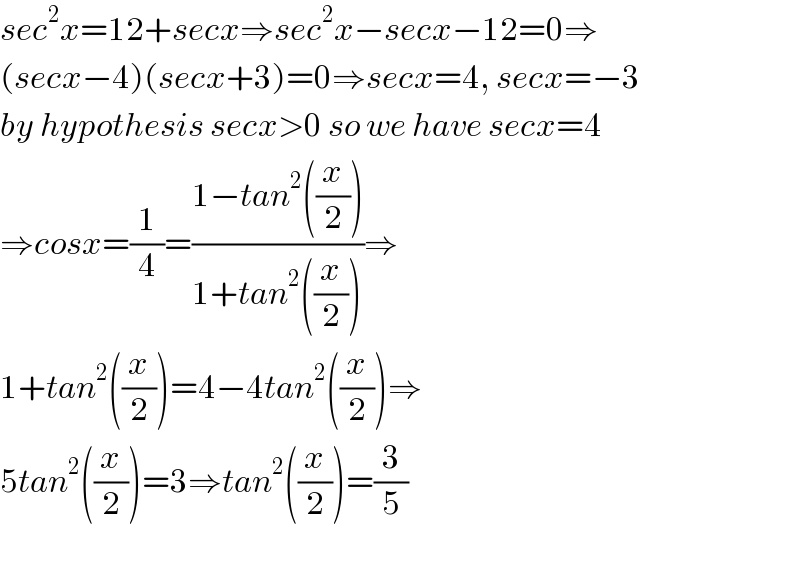
$${sec}^{\mathrm{2}} {x}=\mathrm{12}+{secx}\Rightarrow{sec}^{\mathrm{2}} {x}−{secx}−\mathrm{12}=\mathrm{0}\Rightarrow \\ $$$$\left({secx}−\mathrm{4}\right)\left({secx}+\mathrm{3}\right)=\mathrm{0}\Rightarrow{secx}=\mathrm{4},\:{secx}=−\mathrm{3} \\ $$$${by}\:{hypothesis}\:{secx}>\mathrm{0}\:{so}\:{we}\:{have}\:{secx}=\mathrm{4} \\ $$$$\Rightarrow{cosx}=\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{1}−{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}\Rightarrow \\ $$$$\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)=\mathrm{4}−\mathrm{4}{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\Rightarrow \\ $$$$\mathrm{5}{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)=\mathrm{3}\Rightarrow{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$ \\ $$
Answered by bobhans last updated on 03/Sep/20
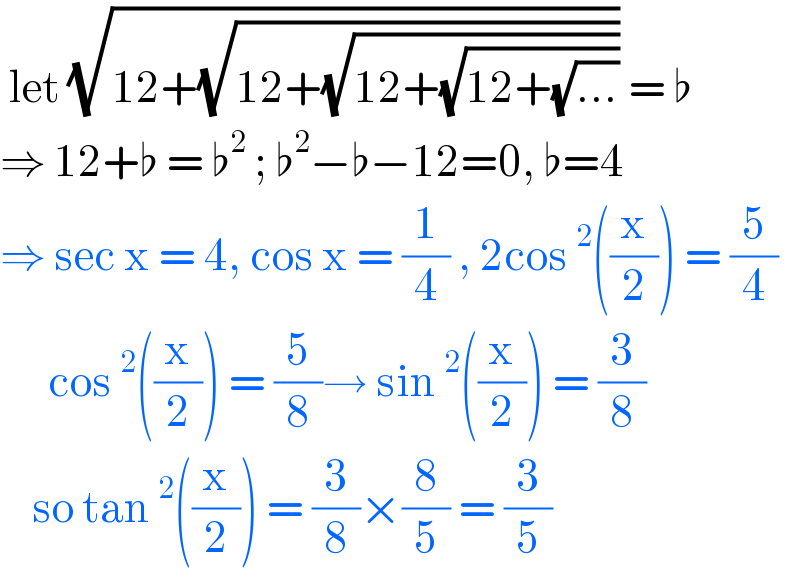
$$\:\mathrm{let}\:\sqrt{\mathrm{12}+\sqrt{\mathrm{12}+\sqrt{\mathrm{12}+\sqrt{\mathrm{12}+\sqrt{…}}}}}\:=\:\flat \\ $$$$\Rightarrow\:\mathrm{12}+\flat\:=\:\flat^{\mathrm{2}} \:;\:\flat^{\mathrm{2}} −\flat−\mathrm{12}=\mathrm{0},\:\flat=\mathrm{4} \\ $$$$\Rightarrow\:\mathrm{sec}\:\mathrm{x}\:=\:\mathrm{4},\:\mathrm{cos}\:\mathrm{x}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\:,\:\mathrm{2cos}\:^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)\:=\:\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\mathrm{cos}\:^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)\:=\:\frac{\mathrm{5}}{\mathrm{8}}\rightarrow\:\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)\:=\:\frac{\mathrm{3}}{\mathrm{8}} \\ $$$$\:\:\:\:\mathrm{so}\:\mathrm{tan}\:^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)\:=\:\frac{\mathrm{3}}{\mathrm{8}}×\frac{\mathrm{8}}{\mathrm{5}}\:=\:\frac{\mathrm{3}}{\mathrm{5}} \\ $$
Commented by peter frank last updated on 03/Sep/20
$${thank}\:{you}\:{both} \\ $$
Answered by Dwaipayan Shikari last updated on 03/Sep/20
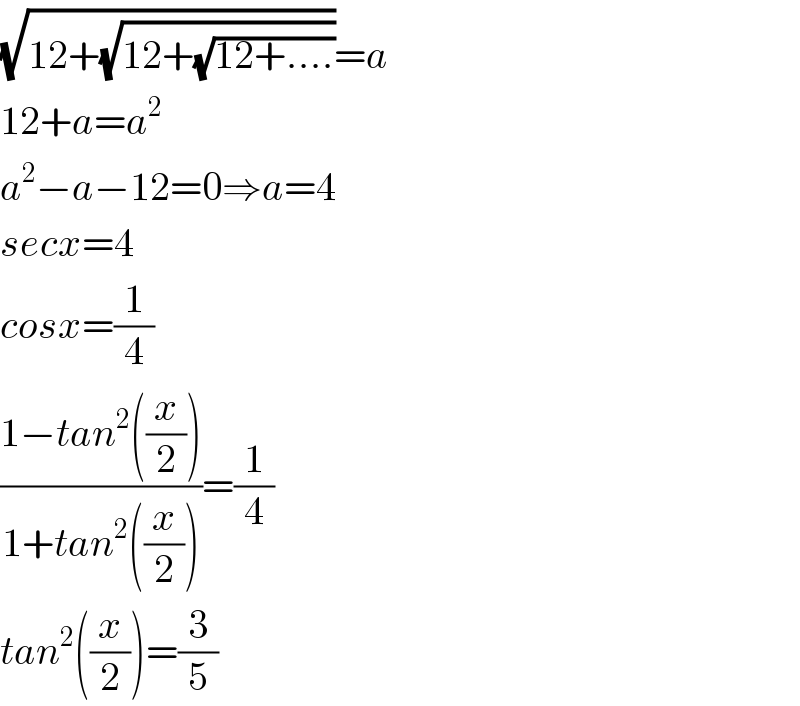
$$\sqrt{\mathrm{12}+\sqrt{\mathrm{12}+\sqrt{\mathrm{12}+….}}}={a} \\ $$$$\mathrm{12}+{a}={a}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} −{a}−\mathrm{12}=\mathrm{0}\Rightarrow{a}=\mathrm{4}\: \\ $$$${secx}=\mathrm{4}\: \\ $$$${cosx}=\frac{\mathrm{1}}{\mathrm{4}}\:\: \\ $$$$\frac{\mathrm{1}−{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}=\frac{\mathrm{1}}{\mathrm{4}}\:\: \\ $$$${tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)=\frac{\mathrm{3}}{\mathrm{5}}\:\:\: \\ $$
