Question Number 111426 by weltr last updated on 03/Sep/20
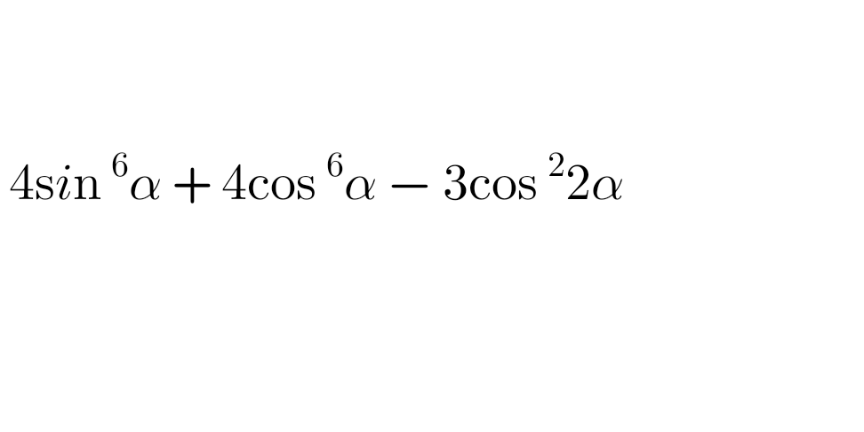
Answered by Dwaipayan Shikari last updated on 03/Sep/20
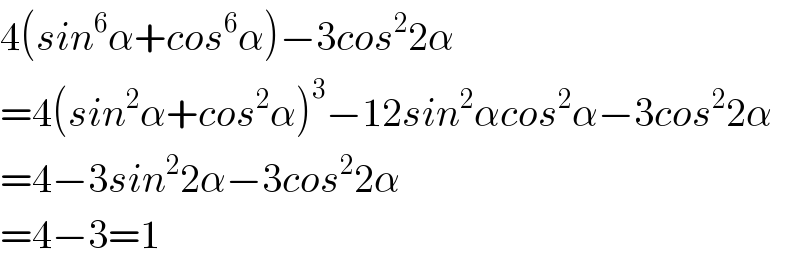
$$\mathrm{4}\left({sin}^{\mathrm{6}} \alpha+{cos}^{\mathrm{6}} \alpha\right)−\mathrm{3}{cos}^{\mathrm{2}} \mathrm{2}\alpha \\ $$$$=\mathrm{4}\left({sin}^{\mathrm{2}} \alpha+{cos}^{\mathrm{2}} \alpha\right)^{\mathrm{3}} −\mathrm{12}{sin}^{\mathrm{2}} \alpha{cos}^{\mathrm{2}} \alpha−\mathrm{3}{cos}^{\mathrm{2}} \mathrm{2}\alpha \\ $$$$=\mathrm{4}−\mathrm{3}{sin}^{\mathrm{2}} \mathrm{2}\alpha−\mathrm{3}{cos}^{\mathrm{2}} \mathrm{2}\alpha \\ $$$$=\mathrm{4}−\mathrm{3}=\mathrm{1} \\ $$
Commented by weltr last updated on 03/Sep/20

$${thank}\:{you} \\ $$
Answered by bobhans last updated on 03/Sep/20
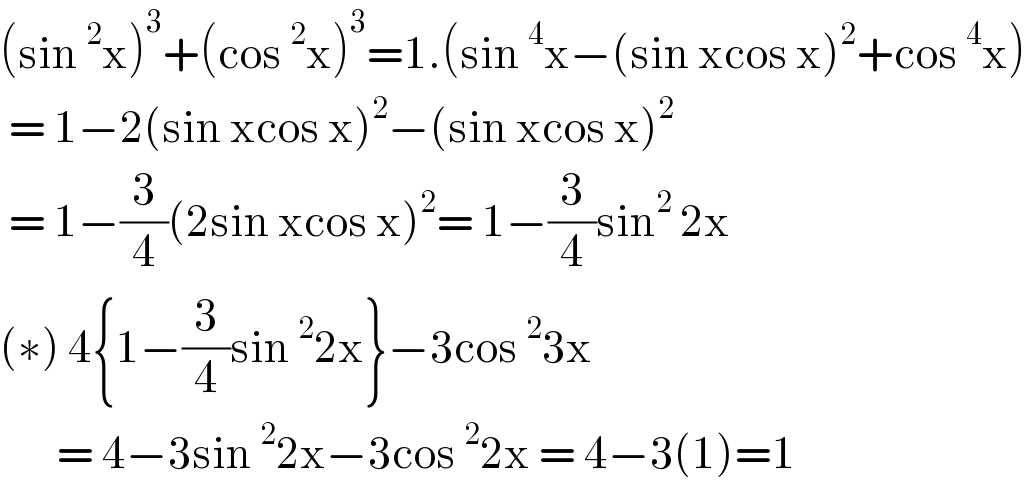
$$\left(\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{3}} +\left(\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{3}} =\mathrm{1}.\left(\mathrm{sin}\:^{\mathrm{4}} \mathrm{x}−\left(\mathrm{sin}\:\mathrm{xcos}\:\mathrm{x}\right)^{\mathrm{2}} +\mathrm{cos}\:^{\mathrm{4}} \mathrm{x}\right) \\ $$$$\:=\:\mathrm{1}−\mathrm{2}\left(\mathrm{sin}\:\mathrm{xcos}\:\mathrm{x}\right)^{\mathrm{2}} −\left(\mathrm{sin}\:\mathrm{xcos}\:\mathrm{x}\right)^{\mathrm{2}} \\ $$$$\:=\:\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}\left(\mathrm{2sin}\:\mathrm{xcos}\:\mathrm{x}\right)^{\mathrm{2}} =\:\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}\mathrm{sin}^{\mathrm{2}} \:\mathrm{2x} \\ $$$$\left(\ast\right)\:\mathrm{4}\left\{\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}\mathrm{sin}\:^{\mathrm{2}} \mathrm{2x}\right\}−\mathrm{3cos}\:^{\mathrm{2}} \mathrm{3x}\: \\ $$$$\:\:\:\:\:\:\:=\:\mathrm{4}−\mathrm{3sin}\:^{\mathrm{2}} \mathrm{2x}−\mathrm{3cos}\:^{\mathrm{2}} \mathrm{2x}\:=\:\mathrm{4}−\mathrm{3}\left(\mathrm{1}\right)=\mathrm{1} \\ $$
Commented by weltr last updated on 03/Sep/20

$${thank}\:{you} \\ $$
