Question-111458

Question Number 111458 by mohammad17 last updated on 03/Sep/20

Commented by kaivan.ahmadi last updated on 03/Sep/20

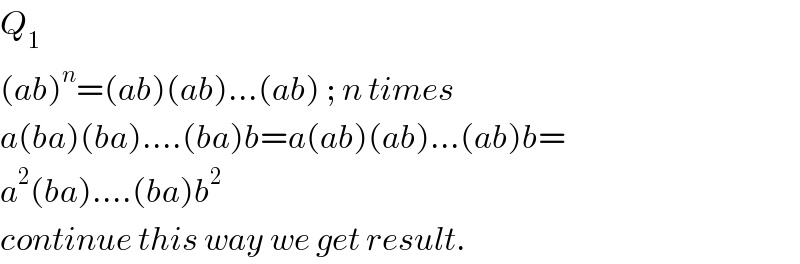
Q_1 (ab)^n =(ab)(ab)...(ab) ; n times a(ba)(ba)....(ba)b=a(ab)(ab)...(ab)b= a^2 (ba)....(ba)b^2 continue this way we get result.

$${Q}_{\mathrm{1}} \\ $$$$\left({ab}\right)^{{n}} =\left({ab}\right)\left({ab}\right)…\left({ab}\right)\:;\:{n}\:{times} \\ $$$${a}\left({ba}\right)\left({ba}\right)….\left({ba}\right){b}={a}\left({ab}\right)\left({ab}\right)…\left({ab}\right){b}= \\ $$$${a}^{\mathrm{2}} \left({ba}\right)….\left({ba}\right){b}^{\mathrm{2}} \\ $$$${continue}\:{this}\:{way}\:{we}\:{get}\:{result}. \\ $$

Commented by kaivan.ahmadi last updated on 04/Sep/20

Q_5 let O(G)=2n for each e≠x∈G⇒∃n: x^(2n) =e⇒(x^n )^2 =e but x^n ∈G. say x^n =a so a^2 =e. [x^n ≠x other wise if x^n =x⇒x^(n−1) =e⇒ o(x)=n−1 that is a contrudiction]

$${Q}_{\mathrm{5}} \\ $$$${let}\:{O}\left({G}\right)=\mathrm{2}{n} \\ $$$${for}\:{each}\:{e}\neq{x}\in{G}\Rightarrow\exists{n}:\:\:{x}^{\mathrm{2}{n}} ={e}\Rightarrow\left({x}^{{n}} \right)^{\mathrm{2}} ={e} \\ $$$${but}\:{x}^{{n}} \in{G}. \\ $$$${say}\:{x}^{{n}} ={a}\:{so}\:{a}^{\mathrm{2}} ={e}. \\ $$$$\left[{x}^{{n}} \neq{x}\:{other}\:{wise}\:{if}\:{x}^{{n}} ={x}\Rightarrow{x}^{{n}−\mathrm{1}} ={e}\Rightarrow\right. \\ $$$$\left.{o}\left({x}\right)={n}−\mathrm{1}\:{that}\:{is}\:{a}\:{contrudiction}\right] \\ $$$$ \\ $$

Commented by kaivan.ahmadi last updated on 03/Sep/20

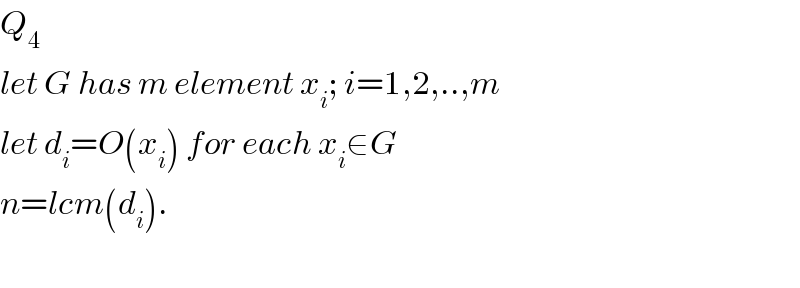
Q_4 let G has m element x_i ; i=1,2,..,m let d_i =O(x_i ) for each x_i ∈G n=lcm(d_i ).

$${Q}_{\mathrm{4}} \\ $$$${let}\:{G}\:{has}\:{m}\:{element}\:{x}_{{i}} ;\:{i}=\mathrm{1},\mathrm{2},..,{m} \\ $$$${let}\:{d}_{{i}} ={O}\left({x}_{{i}} \right)\:{for}\:{each}\:{x}_{{i}} \in{G} \\ $$$${n}={lcm}\left({d}_{{i}} \right). \\ $$$$ \\ $$

Commented by kaivan.ahmadi last updated on 04/Sep/20

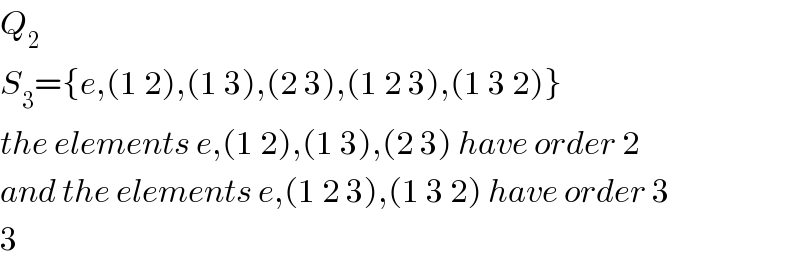
Q_2 S_3 ={e,(1 2),(1 3),(2 3),(1 2 3),(1 3 2)} the elements e,(1 2),(1 3),(2 3) have order 2 and the elements e,(1 2 3),(1 3 2) have order 3 3

$${Q}_{\mathrm{2}} \\ $$$${S}_{\mathrm{3}} =\left\{{e},\left(\mathrm{1}\:\mathrm{2}\right),\left(\mathrm{1}\:\mathrm{3}\right),\left(\mathrm{2}\:\mathrm{3}\right),\left(\mathrm{1}\:\mathrm{2}\:\mathrm{3}\right),\left(\mathrm{1}\:\mathrm{3}\:\mathrm{2}\right)\right\} \\ $$$${the}\:{elements}\:{e},\left(\mathrm{1}\:\mathrm{2}\right),\left(\mathrm{1}\:\mathrm{3}\right),\left(\mathrm{2}\:\mathrm{3}\right)\:{have}\:{order}\:\mathrm{2} \\ $$$${and}\:{the}\:{elements}\:{e},\left(\mathrm{1}\:\mathrm{2}\:\mathrm{3}\right),\left(\mathrm{1}\:\mathrm{3}\:\mathrm{2}\right)\:{have}\:{order}\:\mathrm{3} \\ $$$$\mathrm{3} \\ $$

Commented by kaivan.ahmadi last updated on 04/Sep/20

Q_3 let G={e,a,b} ab≠a sice if ab=a⇒b=e similarly ab≠b so ab=e similarly ba=e and so ab=ba then G is abelian. && the group of order p^2 where p is prime is an abelian group so if O(G)=4=2^2 then G is abelian

$${Q}_{\mathrm{3}} \\ $$$${let}\:{G}=\left\{{e},{a},{b}\right\} \\ $$$${ab}\neq{a}\:{sice}\:{if}\:{ab}={a}\Rightarrow{b}={e}\: \\ $$$${similarly}\:{ab}\neq{b} \\ $$$${so}\:{ab}={e} \\ $$$${similarly}\:{ba}={e}\:{and}\:{so}\:{ab}={ba}\:{then}\:{G}\:{is} \\ $$$${abelian}. \\ $$$$\&\& \\ $$$${the}\:{group}\:{of}\:{order}\:{p}^{\mathrm{2}} \:{where}\:{p}\:{is}\:{prime}\:{is} \\ $$$${an}\:{abelian}\:{group} \\ $$$${so}\:{if}\:{O}\left({G}\right)=\mathrm{4}=\mathrm{2}^{\mathrm{2}} \:{then}\:{G}\:{is}\:{abelian} \\ $$

Commented by kaivan.ahmadi last updated on 04/Sep/20

$$ every group of order 5 is abelian.you can find this theorem in elementary algebra books. && generally every gorup of order less than 6 is abelian.

$$\$\$ \\ $$$${every}\:{group}\:{of}\:{order}\:\mathrm{5}\:{is}\:{abelian}.{you}\:{can} \\ $$$${find}\:{this}\:{theorem}\:{in}\:{elementary}\:{algebra} \\ $$$${books}. \\ $$$$\&\& \\ $$$${generally}\:{every}\:{gorup}\:{of}\:{order}\:{less}\:{than} \\ $$$$\mathrm{6}\:{is}\:{abelian}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply