Question-111497

Question Number 111497 by bemath last updated on 04/Sep/20

Commented by kaivan.ahmadi last updated on 04/Sep/20

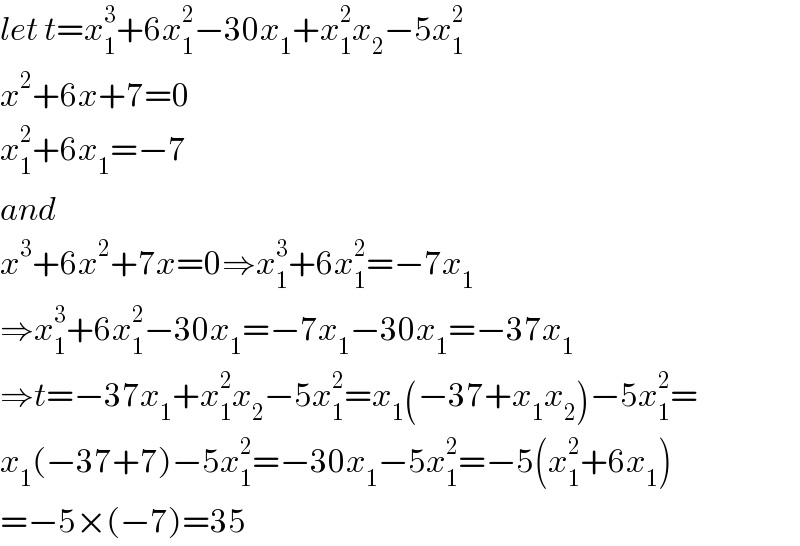
let t=x_1 ^3 +6x_1 ^2 −30x_1 +x_1 ^2 x_2 −5x_1 ^2 x^2 +6x+7=0 x_1 ^2 +6x_1 =−7 and x^3 +6x^2 +7x=0⇒x_1 ^3 +6x_1 ^2 =−7x_1 ⇒x_1 ^3 +6x_1 ^2 −30x_1 =−7x_1 −30x_1 =−37x_1 ⇒t=−37x_1 +x_1 ^2 x_2 −5x_1 ^2 =x_1 (−37+x_1 x_2 )−5x_1 ^2 = x_1 (−37+7)−5x_1 ^2 =−30x_1 −5x_1 ^2 =−5(x_1 ^2 +6x_1 ) =−5×(−7)=35

$${let}\:{t}={x}_{\mathrm{1}} ^{\mathrm{3}} +\mathrm{6}{x}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{30}{x}_{\mathrm{1}} +{x}_{\mathrm{1}} ^{\mathrm{2}} {x}_{\mathrm{2}} −\mathrm{5}{x}_{\mathrm{1}} ^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{7}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{6}{x}_{\mathrm{1}} =−\mathrm{7} \\ $$$${and} \\ $$$${x}^{\mathrm{3}} +\mathrm{6}{x}^{\mathrm{2}} +\mathrm{7}{x}=\mathrm{0}\Rightarrow{x}_{\mathrm{1}} ^{\mathrm{3}} +\mathrm{6}{x}_{\mathrm{1}} ^{\mathrm{2}} =−\mathrm{7}{x}_{\mathrm{1}} \\ $$$$\Rightarrow{x}_{\mathrm{1}} ^{\mathrm{3}} +\mathrm{6}{x}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{30}{x}_{\mathrm{1}} =−\mathrm{7}{x}_{\mathrm{1}} −\mathrm{30}{x}_{\mathrm{1}} =−\mathrm{37}{x}_{\mathrm{1}} \\ $$$$\Rightarrow{t}=−\mathrm{37}{x}_{\mathrm{1}} +{x}_{\mathrm{1}} ^{\mathrm{2}} {x}_{\mathrm{2}} −\mathrm{5}{x}_{\mathrm{1}} ^{\mathrm{2}} ={x}_{\mathrm{1}} \left(−\mathrm{37}+{x}_{\mathrm{1}} {x}_{\mathrm{2}} \right)−\mathrm{5}{x}_{\mathrm{1}} ^{\mathrm{2}} = \\ $$$${x}_{\mathrm{1}} \left(−\mathrm{37}+\mathrm{7}\right)−\mathrm{5}{x}_{\mathrm{1}} ^{\mathrm{2}} =−\mathrm{30}{x}_{\mathrm{1}} −\mathrm{5}{x}_{\mathrm{1}} ^{\mathrm{2}} =−\mathrm{5}\left({x}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{6}{x}_{\mathrm{1}} \right) \\ $$$$=−\mathrm{5}×\left(−\mathrm{7}\right)=\mathrm{35} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply