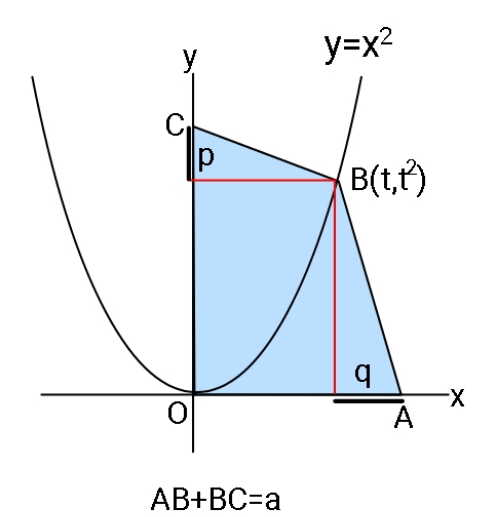
Question Number 111584 by ajfour last updated on 04/Sep/20

Answered by ajfour last updated on 04/Sep/20

$${C}\left(\mathrm{0},{y}\right)\:\:\:;\:{A}\left({x},\mathrm{0}\right)\:\:;\:\:{B}\left({z},{z}^{\mathrm{2}} \right) \\ $$$$\sqrt{\left({x}−{z}\right)^{\mathrm{2}} +{z}^{\mathrm{4}} }+\sqrt{{z}^{\mathrm{2}} +\left({y}−{z}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\:{a} \\ $$$$\bigtriangleup={z}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{2}}{z}\left({y}−{z}^{\mathrm{2}} \right)+\frac{\mathrm{1}}{\mathrm{2}}\left({x}−{z}\right){z}^{\mathrm{2}} \\ $$$${let}\:\:{x}−{z}={z}^{\mathrm{2}} \mathrm{tan}\:\theta \\ $$$$\&\:\:\:\:{y}−{z}^{\mathrm{2}} ={z}\mathrm{tan}\:\phi \\ $$$$\Rightarrow\:\:{z}^{\mathrm{2}} \mathrm{sec}\:\theta+{z}\mathrm{sec}\:\phi={a} \\ $$$$\&\:\:\:\:\bigtriangleup={z}^{\mathrm{3}} +\frac{{z}^{\mathrm{2}} }{\mathrm{2}}\mathrm{tan}\:\phi+\frac{{z}^{\mathrm{4}} }{\mathrm{2}}\mathrm{tan}\:\theta \\ $$$$\:{someone}\:{please}\:{help}.. \\ $$
Commented by mr W last updated on 05/Sep/20

$${P}={z}^{\mathrm{3}} +\frac{{z}^{\mathrm{2}} }{\mathrm{2}}\mathrm{tan}\:\phi+\frac{{z}^{\mathrm{4}} }{\mathrm{2}}\mathrm{tan}\:\theta+\lambda\left({z}^{\mathrm{2}} \mathrm{sec}\:\theta+{z}\mathrm{sec}\phi−{a}\right) \\ $$$$\frac{\partial{P}}{\partial{z}}=\mathrm{0},\:\frac{\partial{P}}{\partial\theta}=\mathrm{0},\:\frac{\partial{P}}{\partial\phi}=\mathrm{0},\:\frac{\partial{P}}{\partial\lambda}=\mathrm{0} \\ $$$$….\:{hard}\:{to}\:{solve}\:… \\ $$
Answered by ajfour last updated on 06/Sep/20