Question Number 111650 by mohammad17 last updated on 04/Sep/20

Commented by mohammad17 last updated on 04/Sep/20
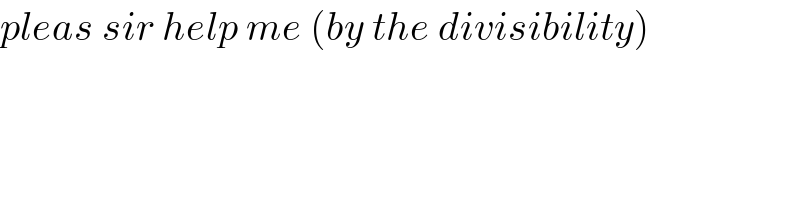
$${pleas}\:{sir}\:{help}\:{me}\:\left({by}\:{the}\:{divisibility}\right) \\ $$
Commented by mohammad17 last updated on 04/Sep/20

$${are}\:{you}\:{can}\:{help} \\ $$
Answered by Her_Majesty last updated on 04/Sep/20
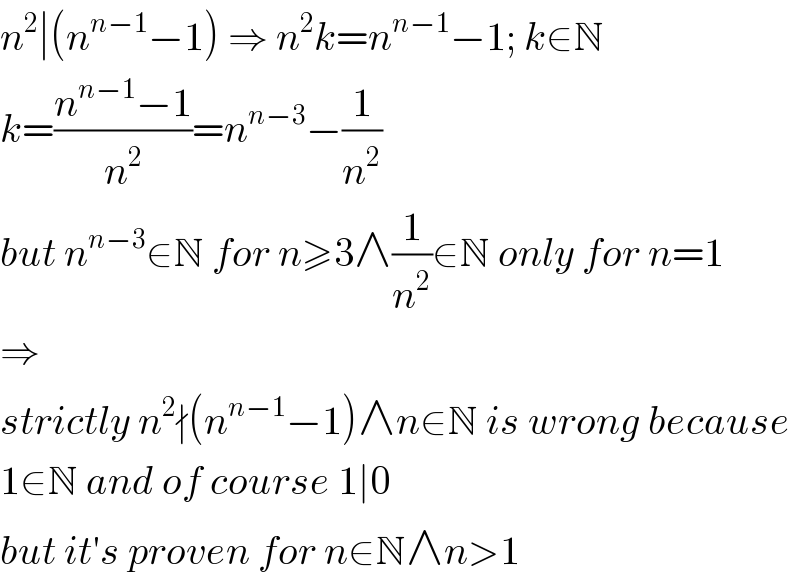
$${n}^{\mathrm{2}} \mid\left({n}^{{n}−\mathrm{1}} −\mathrm{1}\right)\:\Rightarrow\:{n}^{\mathrm{2}} {k}={n}^{{n}−\mathrm{1}} −\mathrm{1};\:{k}\in\mathbb{N} \\ $$$${k}=\frac{{n}^{{n}−\mathrm{1}} −\mathrm{1}}{{n}^{\mathrm{2}} }={n}^{{n}−\mathrm{3}} −\frac{\mathrm{1}}{{n}^{\mathrm{2}} } \\ $$$${but}\:{n}^{{n}−\mathrm{3}} \in\mathbb{N}\:{for}\:{n}\geqslant\mathrm{3}\wedge\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\in\mathbb{N}\:{only}\:{for}\:{n}=\mathrm{1} \\ $$$$\Rightarrow \\ $$$${strictly}\:{n}^{\mathrm{2}} \nmid\left({n}^{{n}−\mathrm{1}} −\mathrm{1}\right)\wedge{n}\in\mathbb{N}\:{is}\:{wrong}\:{because} \\ $$$$\mathrm{1}\in\mathbb{N}\:{and}\:{of}\:{course}\:\mathrm{1}\mid\mathrm{0} \\ $$$${but}\:{it}'{s}\:{proven}\:{for}\:{n}\in\mathbb{N}\wedge{n}>\mathrm{1} \\ $$
Commented by mohammad17 last updated on 04/Sep/20

$${thank}\:{you}\:{sir} \\ $$
