Question Number 111745 by mohammad17 last updated on 04/Sep/20

Commented by mohammad17 last updated on 04/Sep/20

$${help}\:{me}\:{sir} \\ $$
Commented by Aziztisffola last updated on 05/Sep/20
![∫_(100) ^( ∞) 0.002e^(−0.002x) dx=[−e^(−0.002x) ]_(100) ^∞ =e^(−0.002×100) =e^(−0.2) =...](https://www.tinkutara.com/question/Q111807.png)
$$\int_{\mathrm{100}} ^{\:\infty} \mathrm{0}.\mathrm{002e}^{−\mathrm{0}.\mathrm{002x}} \mathrm{dx}=\left[−\mathrm{e}^{−\mathrm{0}.\mathrm{002x}} \right]_{\mathrm{100}} ^{\infty} \\ $$$$=\mathrm{e}^{−\mathrm{0}.\mathrm{002}×\mathrm{100}} =\mathrm{e}^{−\mathrm{0}.\mathrm{2}} =… \\ $$
Commented by Aziztisffola last updated on 04/Sep/20
![1 .∫_0 ^( +∞) f(x)dx=1 2. a) F(x)=p(]−∞;x])=1−e^(−λx) b) ∫_(25) ^( ∞) f(x)dx=0.9512 ⇒λ=0.002](https://www.tinkutara.com/question/Q111778.png)
$$\mathrm{1}\:.\int_{\mathrm{0}} ^{\:+\infty} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\mathrm{1} \\ $$$$\left.\mathrm{2}\left..\left.\:\:\mathrm{a}\right)\:\mathrm{F}\left(\mathrm{x}\right)=\mathrm{p}\left(\right]−\infty;\mathrm{x}\right]\right)=\mathrm{1}−\mathrm{e}^{−\lambda\mathrm{x}} \\ $$$$\left.\mathrm{b}\right)\:\int_{\mathrm{25}} ^{\:\infty} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\mathrm{0}.\mathrm{9512} \\ $$$$\Rightarrow\lambda=\mathrm{0}.\mathrm{002} \\ $$
Commented by mohammad17 last updated on 04/Sep/20

$${thank}\:{you}\:{sir}\:{can}\:{you}\:{complete}\:{the}\:{solutions}\:{of}\:{all}\:{question}\:{please}\:? \\ $$
Commented by Aziztisffola last updated on 04/Sep/20
![2 b) ∫_(25) ^∞ λe^(−λx) dx=0.9512 ⇒[−e^(−λx) ]_(25) ^∞ =0.9512 ⇒e^(−25λ) =0.9512 ⇒−25λ=ln(0.9512) λ=((ln(0.9512))/(−25))=0.002 3.a) p(X≥100)=∫_(100) ^∞ 0.002e^(−0.002x) dx=... b) p_((X≥100)) (X≥150)=((p(X≥150))/(p(X≥100)))=...](https://www.tinkutara.com/question/Q111793.png)
$$\left.\mathrm{2}\:\mathrm{b}\right)\:\int_{\mathrm{25}} ^{\infty} \lambda\mathrm{e}^{−\lambda\mathrm{x}} \mathrm{dx}=\mathrm{0}.\mathrm{9512} \\ $$$$\Rightarrow\left[−\mathrm{e}^{−\lambda\mathrm{x}} \right]_{\mathrm{25}} ^{\infty} =\mathrm{0}.\mathrm{9512} \\ $$$$\Rightarrow\mathrm{e}^{−\mathrm{25}\lambda} =\mathrm{0}.\mathrm{9512} \\ $$$$\Rightarrow−\mathrm{25}\lambda=\mathrm{ln}\left(\mathrm{0}.\mathrm{9512}\right) \\ $$$$\lambda=\frac{\mathrm{ln}\left(\mathrm{0}.\mathrm{9512}\right)}{−\mathrm{25}}=\mathrm{0}.\mathrm{002} \\ $$$$\left.\mathrm{3}.\mathrm{a}\right)\:\mathrm{p}\left(\mathrm{X}\geqslant\mathrm{100}\right)=\int_{\mathrm{100}} ^{\infty} \mathrm{0}.\mathrm{002e}^{−\mathrm{0}.\mathrm{002x}} \mathrm{dx}=… \\ $$$$\left.\mathrm{b}\right)\:\mathrm{p}_{\left(\mathrm{X}\geqslant\mathrm{100}\right)} \left(\mathrm{X}\geqslant\mathrm{150}\right)=\frac{\mathrm{p}\left(\mathrm{X}\geqslant\mathrm{150}\right)}{\mathrm{p}\left(\mathrm{X}\geqslant\mathrm{100}\right)}=… \\ $$
Commented by mohammad17 last updated on 05/Sep/20
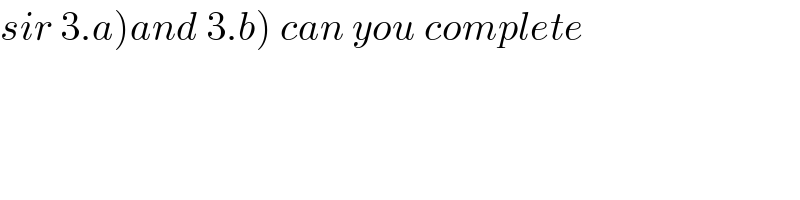
$$\left.{s}\left.{ir}\:\mathrm{3}.{a}\right){and}\:\mathrm{3}.{b}\right)\:{can}\:{you}\:{complete} \\ $$
