Question-111774

Question Number 111774 by I want to learn more last updated on 04/Sep/20

Answered by mr W last updated on 04/Sep/20

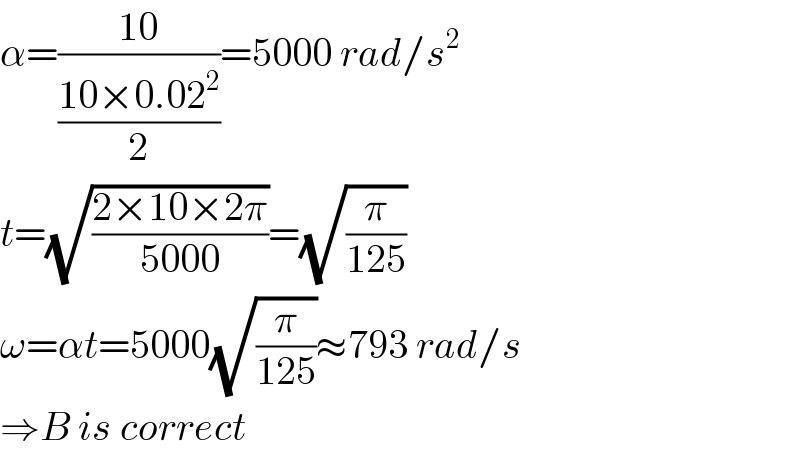
α=((10)/((10×0.02^2 )/2))=5000 rad/s^2 t=(√((2×10×2π)/(5000)))=(√(π/(125))) ω=αt=5000(√(π/(125)))≈793 rad/s ⇒B is correct

$$\alpha=\frac{\mathrm{10}}{\frac{\mathrm{10}×\mathrm{0}.\mathrm{02}^{\mathrm{2}} }{\mathrm{2}}}=\mathrm{5000}\:{rad}/{s}^{\mathrm{2}} \\ $$$${t}=\sqrt{\frac{\mathrm{2}×\mathrm{10}×\mathrm{2}\pi}{\mathrm{5000}}}=\sqrt{\frac{\pi}{\mathrm{125}}} \\ $$$$\omega=\alpha{t}=\mathrm{5000}\sqrt{\frac{\pi}{\mathrm{125}}}\approx\mathrm{793}\:{rad}/{s} \\ $$$$\Rightarrow{B}\:{is}\:{correct} \\ $$

Commented by mr W last updated on 05/Sep/20

$${and} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{I}\omega^{\mathrm{2}} =\Gamma\Delta\theta \\ $$

Commented by Dwaipayan Shikari last updated on 04/Sep/20

$${Yes}\:{sir}! \\ $$

Commented by mr W last updated on 04/Sep/20

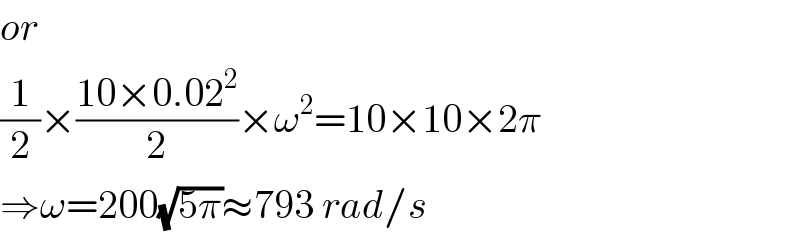
or (1/2)×((10×0.02^2 )/2)×ω^2 =10×10×2π ⇒ω=200(√(5π))≈793 rad/s

$${or} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{10}×\mathrm{0}.\mathrm{02}^{\mathrm{2}} }{\mathrm{2}}×\omega^{\mathrm{2}} =\mathrm{10}×\mathrm{10}×\mathrm{2}\pi \\ $$$$\Rightarrow\omega=\mathrm{200}\sqrt{\mathrm{5}\pi}\approx\mathrm{793}\:{rad}/{s} \\ $$

Commented by I want to learn more last updated on 04/Sep/20

Thanks sir, i really appreciate. sir, please what formular do you use to find α and t

$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}. \\ $$$$\mathrm{sir},\:\mathrm{please}\:\mathrm{what}\:\mathrm{formular}\:\mathrm{do}\:\mathrm{you}\:\mathrm{use}\:\mathrm{to}\:\mathrm{find}\:\:\alpha\:\:\mathrm{and}\:\:\mathrm{t} \\ $$

Commented by Dwaipayan Shikari last updated on 04/Sep/20

Γ_(torque) =∣Iα^→ ∣ I=moment of inertia Here moment of inertia is (1/2)MR^2 α=((2Γ_(torque) )/(MR^2 )) ( Γ=∣F^→ ×R^→ ∣=FRsinθ=MaR=MR.α.R=I.α) a=Rα (Rotational analogue) (θ=(π/2) here) θ_1 −θ_0 =w_0 t+(1/2)αt^2 (w_0 =0) △θ=(1/2)αt^2 t=(√((2△θ)/α))

$$\Gamma_{{torque}} =\mid{I}\overset{\rightarrow} {\alpha}\mid\:\:{I}={moment}\:{of}\:{inertia} \\ $$$${Here}\:{moment}\:{of}\:{inertia}\:{is}\:\frac{\mathrm{1}}{\mathrm{2}}{MR}^{\mathrm{2}} \\ $$$$\alpha=\frac{\mathrm{2}\Gamma_{{torque}} }{{MR}^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:\left(\:\:\:\:\:\Gamma=\mid\overset{\rightarrow} {{F}}×\overset{\rightarrow} {{R}}\mid={FRsin}\theta={MaR}={MR}.\alpha.{R}={I}.\alpha\right) \\ $$$${a}={R}\alpha\:\left({Rotational}\:{analogue}\right)\:\:\:\left(\theta=\frac{\pi}{\mathrm{2}}\:{here}\right) \\ $$$$\theta_{\mathrm{1}} −\theta_{\mathrm{0}} ={w}_{\mathrm{0}} {t}+\frac{\mathrm{1}}{\mathrm{2}}\alpha{t}^{\mathrm{2}} \:\:\left({w}_{\mathrm{0}} =\mathrm{0}\right)\:\:\:\:\:\:\:\: \\ $$$$\bigtriangleup\theta=\frac{\mathrm{1}}{\mathrm{2}}\alpha{t}^{\mathrm{2}} \\ $$$${t}=\sqrt{\frac{\mathrm{2}\bigtriangleup\theta}{\alpha}} \\ $$

Commented by I want to learn more last updated on 05/Sep/20

$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply