Menu Close

Question-111799

Tinku Tara 0 Comments
Pin




Question Number 111799 by ajfour last updated on 05/Sep/20
Commented by mr W last updated on 05/Sep/20
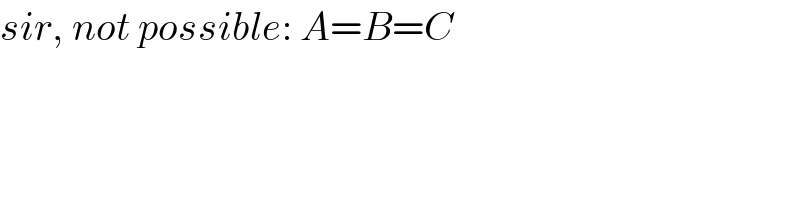
sir, not possible: A=B=C
$${sir},\:{not}\:{possible}:\:{A}={B}={C} \\ $$
Commented by ajfour last updated on 05/Sep/20
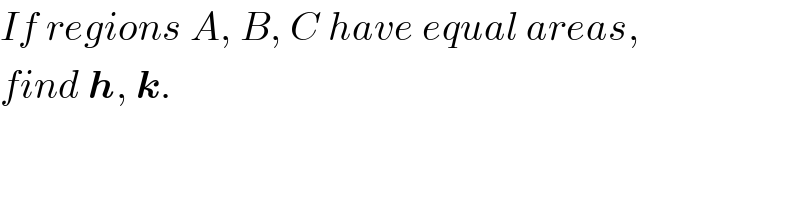
If regions A, B, C have equal areas, find h, k.
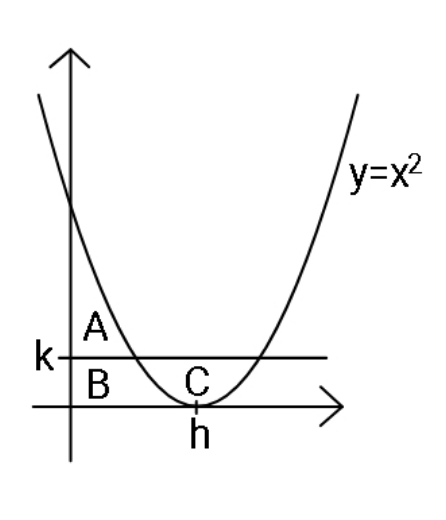
$${If}\:{regions}\:{A},\:{B},\:{C}\:{have}\:{equal}\:{areas}, \\ $$$${find}\:\boldsymbol{{h}},\:\boldsymbol{{k}}. \\ $$
Commented by ajfour last updated on 05/Sep/20
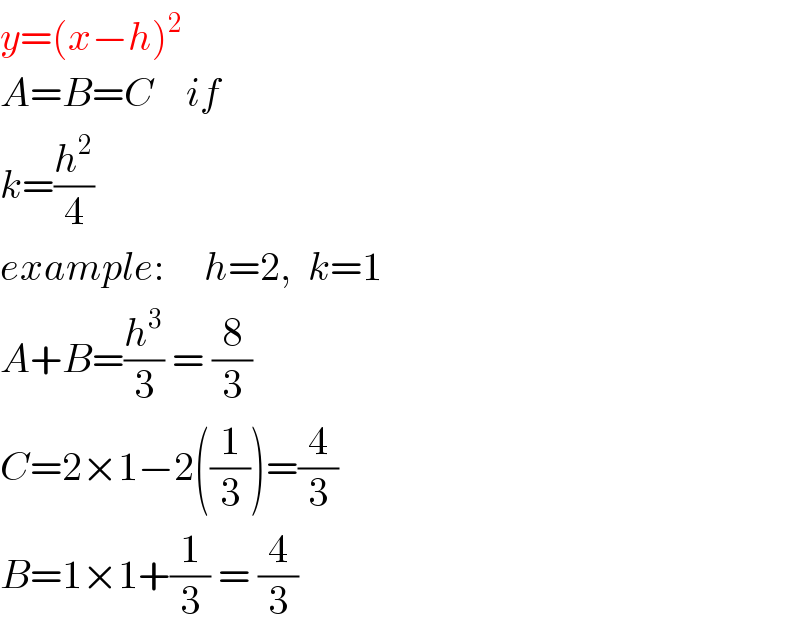
y=(x−h)^2 A=B=C if k=(h^2 /4) example: h=2, k=1 A+B=(h^3 /3) = (8/3) C=2×1−2((1/3))=(4/3) B=1×1+(1/3) = (4/3)
$${y}=\left({x}−{h}\right)^{\mathrm{2}} \\ $$$${A}={B}={C}\:\:\:\:{if} \\ $$$${k}=\frac{{h}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${example}:\:\:\:\:\:{h}=\mathrm{2},\:\:{k}=\mathrm{1} \\ $$$${A}+{B}=\frac{{h}^{\mathrm{3}} }{\mathrm{3}}\:=\:\frac{\mathrm{8}}{\mathrm{3}} \\ $$$${C}=\mathrm{2}×\mathrm{1}−\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${B}=\mathrm{1}×\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\:=\:\frac{\mathrm{4}}{\mathrm{3}} \\ $$
Commented by mr W last updated on 05/Sep/20
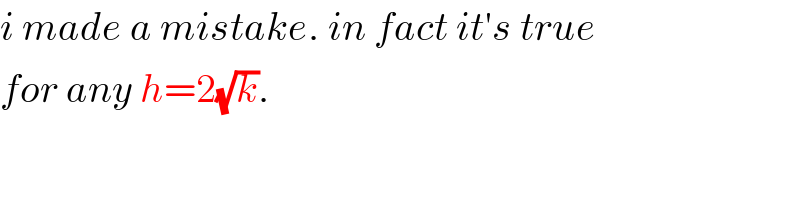
i made a mistake. in fact it′s true for any h=2(√k).
$${i}\:{made}\:{a}\:{mistake}.\:{in}\:{fact}\:{it}'{s}\:{true} \\ $$$${for}\:{any}\:{h}=\mathrm{2}\sqrt{{k}}. \\ $$
Answered by 1549442205PVT last updated on 05/Sep/20
Answered by mr W last updated on 05/Sep/20
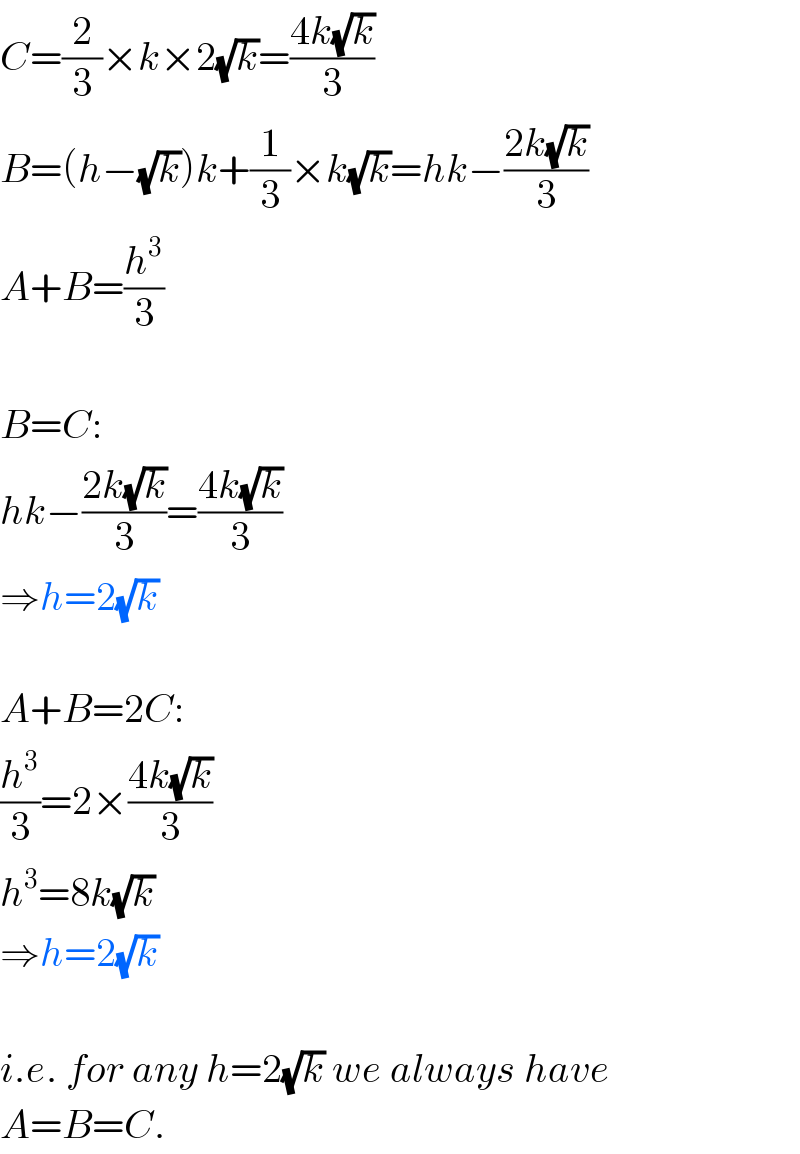
C=(2/3)×k×2(√k)=((4k(√k))/3) B=(h−(√k))k+(1/3)×k(√k)=hk−((2k(√k))/3) A+B=(h^3 /3) B=C: hk−((2k(√k))/3)=((4k(√k))/3) ⇒h=2(√k) A+B=2C: (h^3 /3)=2×((4k(√k))/3) h^3 =8k(√k) ⇒h=2(√k) i.e. for any h=2(√k) we always have A=B=C.
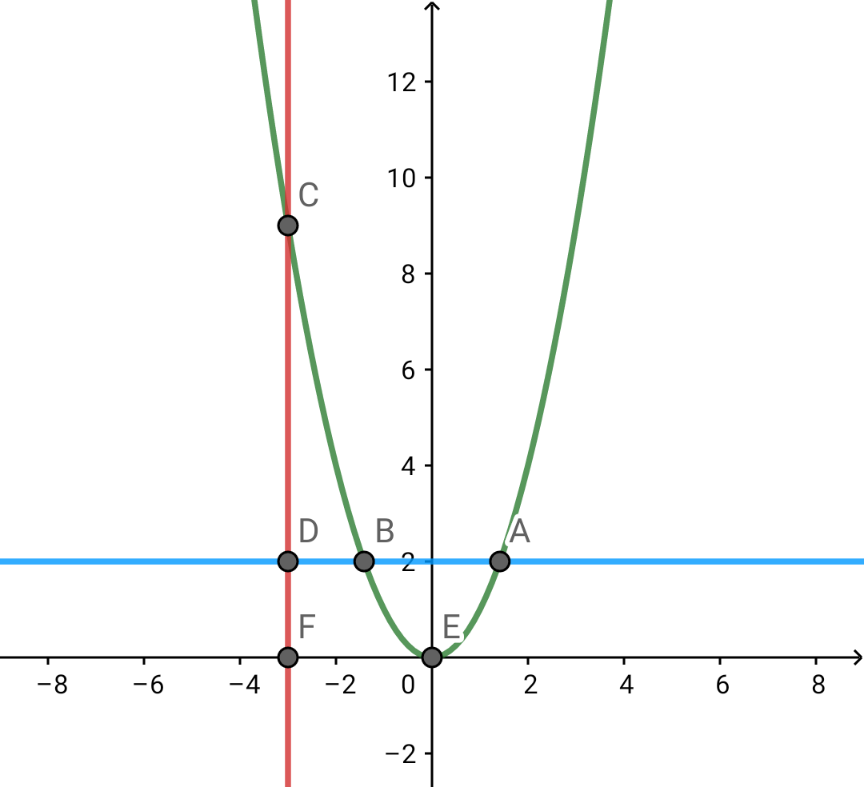
$${C}=\frac{\mathrm{2}}{\mathrm{3}}×{k}×\mathrm{2}\sqrt{{k}}=\frac{\mathrm{4}{k}\sqrt{{k}}}{\mathrm{3}} \\ $$$${B}=\left({h}−\sqrt{{k}}\right){k}+\frac{\mathrm{1}}{\mathrm{3}}×{k}\sqrt{{k}}={hk}−\frac{\mathrm{2}{k}\sqrt{{k}}}{\mathrm{3}} \\ $$$${A}+{B}=\frac{{h}^{\mathrm{3}} }{\mathrm{3}} \\ $$$$ \\ $$$${B}={C}: \\ $$$${hk}−\frac{\mathrm{2}{k}\sqrt{{k}}}{\mathrm{3}}=\frac{\mathrm{4}{k}\sqrt{{k}}}{\mathrm{3}} \\ $$$$\Rightarrow{h}=\mathrm{2}\sqrt{{k}} \\ $$$$ \\ $$$${A}+{B}=\mathrm{2}{C}: \\ $$$$\frac{{h}^{\mathrm{3}} }{\mathrm{3}}=\mathrm{2}×\frac{\mathrm{4}{k}\sqrt{{k}}}{\mathrm{3}} \\ $$$${h}^{\mathrm{3}} =\mathrm{8}{k}\sqrt{{k}} \\ $$$$\Rightarrow{h}=\mathrm{2}\sqrt{{k}} \\ $$$$ \\ $$$${i}.{e}.\:{for}\:{any}\:{h}=\mathrm{2}\sqrt{{k}}\:{we}\:{always}\:{have} \\ $$$${A}={B}={C}. \\ $$
Commented by ajfour last updated on 05/Sep/20
Yes! Thanks Sir.
$${Yes}!\:\mathcal{T}{hanks}\:{Sir}. \\ $$
Answered by 1549442205PVT last updated on 05/Sep/20
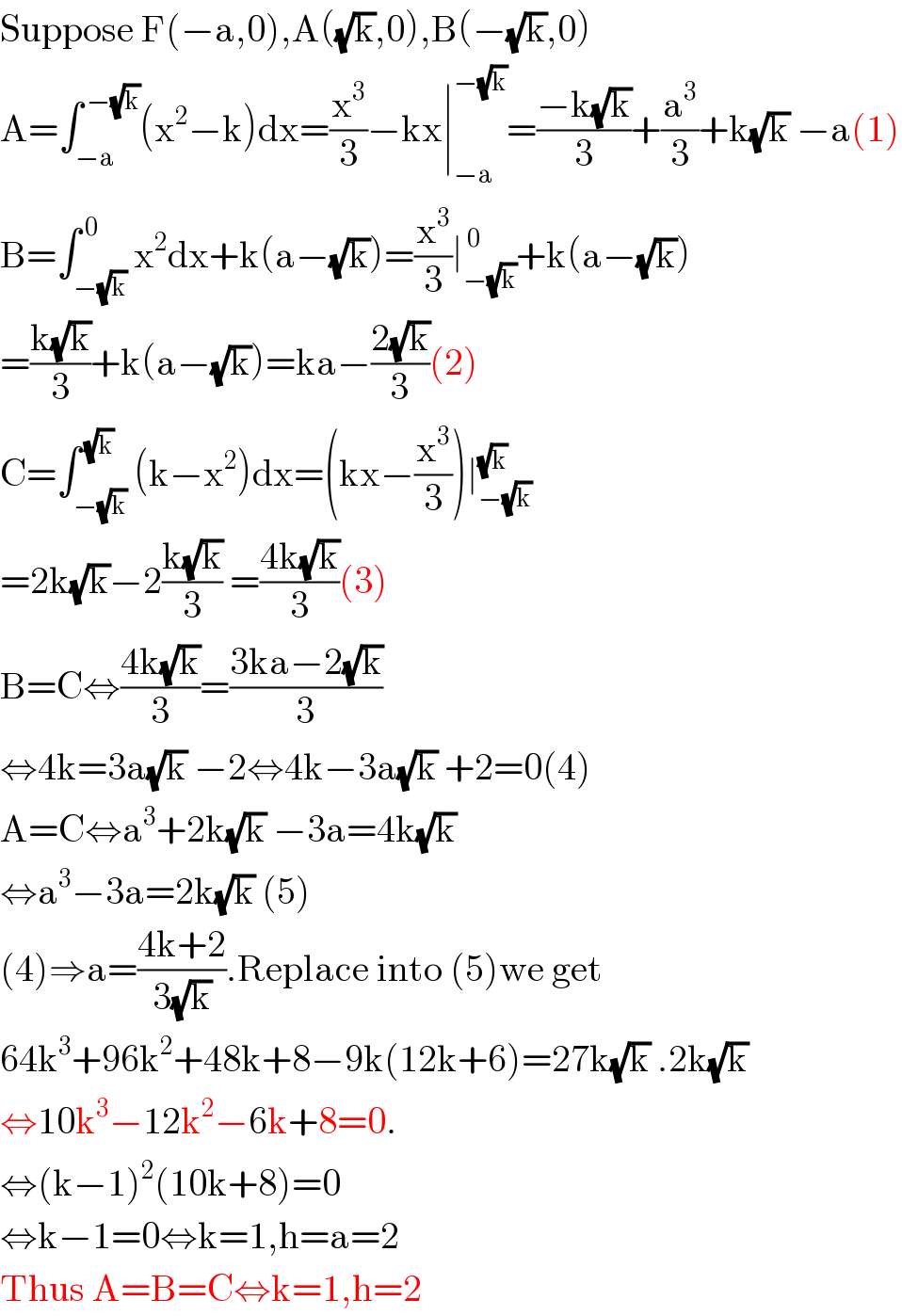
Suppose F(−a,0),A((√k),0),B(−(√k),0) A=∫_(−a) ^( −(√k)) (x^2 −k)dx=(x^3 /3)−kx∣_(−a) ^(−(√k)) =((−k(√k))/3)+(a^3 /3)+k(√k) −a(1) B=∫_(−(√k)) ^( 0) x^2 dx+k(a−(√k))=(x^3 /3)∣_(−(√k)) ^( 0) +k(a−(√k)) =((k(√k))/3)+k(a−(√k))=ka−((2(√k))/3)(2) C=∫_(−(√k)) ^( (√k)) (k−x^2 )dx=(kx−(x^3 /3))∣_(−(√k)) ^(√k) =2k(√k)−2((k(√k))/3) =((4k(√k))/3)(3) B=C⇔((4k(√k))/3)=((3ka−2(√k))/3) ⇔4k=3a(√k) −2⇔4k−3a(√k) +2=0(4) A=C⇔a^3 +2k(√k) −3a=4k(√k) ⇔a^3 −3a=2k(√k) (5) (4)⇒a=((4k+2)/(3(√k))).Replace into (5)we get 64k^3 +96k^2 +48k+8−9k(12k+6)=27k(√k) .2k(√k) ⇔10k^3 −12k^2 −6k+8=0. ⇔(k−1)^2 (10k+8)=0 ⇔k−1=0⇔k=1,h=a=2 Thus A=B=C⇔k=1,h=2
$$\mathrm{Suppose}\:\mathrm{F}\left(−\mathrm{a},\mathrm{0}\right),\mathrm{A}\left(\sqrt{\mathrm{k}},\mathrm{0}\right),\mathrm{B}\left(−\sqrt{\mathrm{k}},\mathrm{0}\right) \\ $$$$\mathrm{A}=\int_{−\mathrm{a}} ^{\:−\sqrt{\mathrm{k}}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{k}\right)\mathrm{dx}=\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}−\mathrm{kx}\mid_{−\mathrm{a}} ^{−\sqrt{\mathrm{k}}} =\frac{−\mathrm{k}\sqrt{\mathrm{k}}}{\mathrm{3}}+\frac{\mathrm{a}^{\mathrm{3}} }{\mathrm{3}}+\mathrm{k}\sqrt{\mathrm{k}}\:−\mathrm{a}\left(\mathrm{1}\right) \\ $$$$\mathrm{B}=\int_{−\sqrt{\mathrm{k}}} ^{\:\mathrm{0}} \mathrm{x}^{\mathrm{2}} \mathrm{dx}+\mathrm{k}\left(\mathrm{a}−\sqrt{\mathrm{k}}\right)=\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}\mid_{−\sqrt{\mathrm{k}}} ^{\:\mathrm{0}} +\mathrm{k}\left(\mathrm{a}−\sqrt{\mathrm{k}}\right) \\ $$$$=\frac{\mathrm{k}\sqrt{\mathrm{k}}}{\mathrm{3}}+\mathrm{k}\left(\mathrm{a}−\sqrt{\mathrm{k}}\right)=\mathrm{ka}−\frac{\mathrm{2}\sqrt{\mathrm{k}}}{\mathrm{3}}\left(\mathrm{2}\right) \\ $$$$\mathrm{C}=\int_{−\sqrt{\mathrm{k}}} ^{\:\sqrt{\mathrm{k}}} \left(\mathrm{k}−\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx}=\left(\mathrm{kx}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}\right)\mid_{−\sqrt{\mathrm{k}}} ^{\sqrt{\mathrm{k}}} \\ $$$$=\mathrm{2k}\sqrt{\mathrm{k}}−\mathrm{2}\frac{\mathrm{k}\sqrt{\mathrm{k}}}{\mathrm{3}}\:=\frac{\mathrm{4k}\sqrt{\mathrm{k}}}{\mathrm{3}}\left(\mathrm{3}\right) \\ $$$$\mathrm{B}=\mathrm{C}\Leftrightarrow\frac{\mathrm{4k}\sqrt{\mathrm{k}}}{\mathrm{3}}=\frac{\mathrm{3ka}−\mathrm{2}\sqrt{\mathrm{k}}}{\mathrm{3}} \\ $$$$\Leftrightarrow\mathrm{4k}=\mathrm{3a}\sqrt{\mathrm{k}}\:−\mathrm{2}\Leftrightarrow\mathrm{4k}−\mathrm{3a}\sqrt{\mathrm{k}}\:+\mathrm{2}=\mathrm{0}\left(\mathrm{4}\right) \\ $$$$\mathrm{A}=\mathrm{C}\Leftrightarrow\mathrm{a}^{\mathrm{3}} +\mathrm{2k}\sqrt{\mathrm{k}}\:−\mathrm{3a}=\mathrm{4k}\sqrt{\mathrm{k}}\: \\ $$$$\Leftrightarrow\mathrm{a}^{\mathrm{3}} −\mathrm{3a}=\mathrm{2k}\sqrt{\mathrm{k}}\:\left(\mathrm{5}\right) \\ $$$$\left(\mathrm{4}\right)\Rightarrow\mathrm{a}=\frac{\mathrm{4k}+\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{k}}}.\mathrm{Replace}\:\mathrm{into}\:\left(\mathrm{5}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{64k}^{\mathrm{3}} +\mathrm{96k}^{\mathrm{2}} +\mathrm{48k}+\mathrm{8}−\mathrm{9k}\left(\mathrm{12k}+\mathrm{6}\right)=\mathrm{27k}\sqrt{\mathrm{k}}\:.\mathrm{2k}\sqrt{\mathrm{k}} \\ $$$$\Leftrightarrow\mathrm{10k}^{\mathrm{3}} −\mathrm{12k}^{\mathrm{2}} −\mathrm{6k}+\mathrm{8}=\mathrm{0}. \\ $$$$\Leftrightarrow\left(\mathrm{k}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{10k}+\mathrm{8}\right)=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{k}−\mathrm{1}=\mathrm{0}\Leftrightarrow\mathrm{k}=\mathrm{1},\mathrm{h}=\mathrm{a}=\mathrm{2} \\ $$$$\mathrm{Thus}\:\mathrm{A}=\mathrm{B}=\mathrm{C}\Leftrightarrow\mathrm{k}=\mathrm{1},\mathrm{h}=\mathrm{2} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *