Menu Close

Question-111974

Tinku Tara 0 Comments
Pin




Question Number 111974 by mohammad17 last updated on 05/Sep/20
Answered by mathmax by abdo last updated on 05/Sep/20
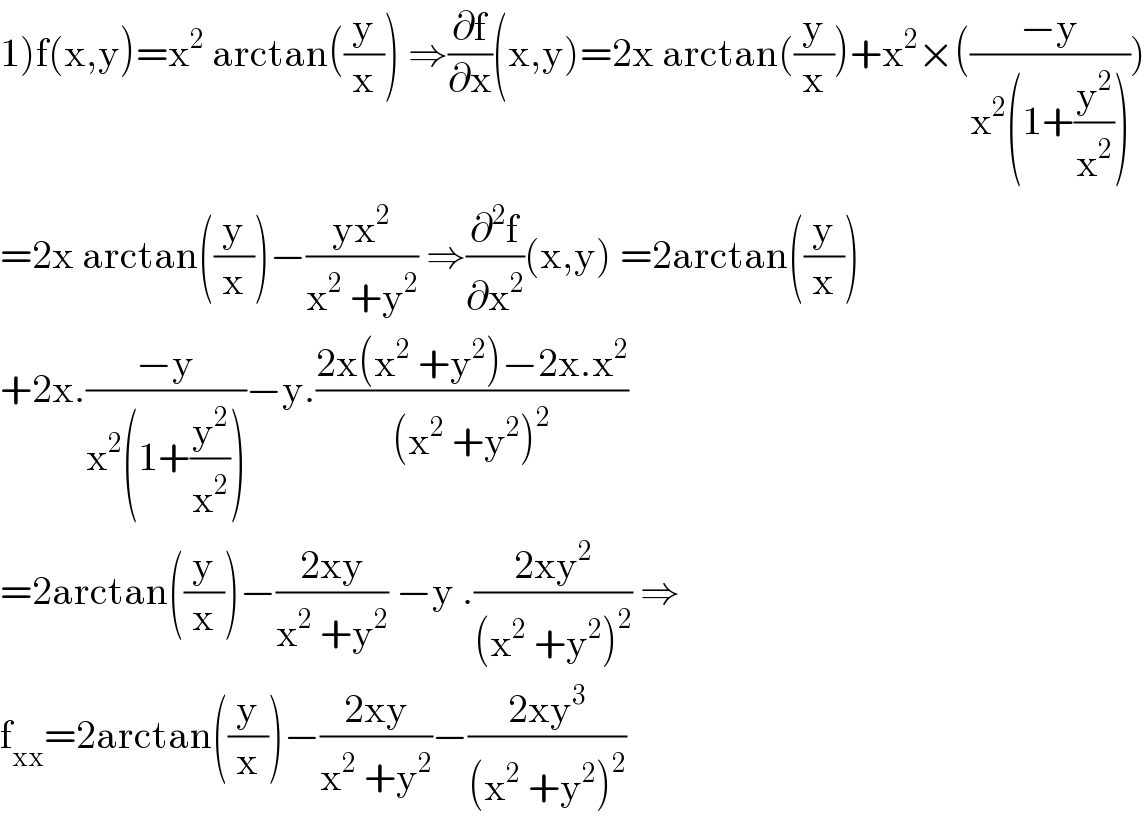
1)f(x,y)=x^2 arctan((y/x)) ⇒(∂f/∂x)(x,y)=2x arctan((y/x))+x^2 ×(((−y)/(x^2 (1+(y^2 /x^2 ))))) =2x arctan((y/x))−((yx^2 )/(x^2 +y^2 )) ⇒(∂^2 f/∂x^2 )(x,y) =2arctan((y/x)) +2x.((−y)/(x^2 (1+(y^2 /x^2 ))))−y.((2x(x^2 +y^2 )−2x.x^2 )/((x^2 +y^2 )^2 )) =2arctan((y/x))−((2xy)/(x^2 +y^2 )) −y .((2xy^2 )/((x^2 +y^2 )^2 )) ⇒ f_(xx) =2arctan((y/x))−((2xy)/(x^2 +y^2 ))−((2xy^3 )/((x^2 +y^2 )^2 ))
$$\left.\mathrm{1}\right)\mathrm{f}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{x}^{\mathrm{2}} \:\mathrm{arctan}\left(\frac{\mathrm{y}}{\mathrm{x}}\right)\:\Rightarrow\frac{\partial\mathrm{f}}{\partial\mathrm{x}}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{2x}\:\mathrm{arctan}\left(\frac{\mathrm{y}}{\mathrm{x}}\right)+\mathrm{x}^{\mathrm{2}} ×\left(\frac{−\mathrm{y}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }\right)}\right) \\ $$$$=\mathrm{2x}\:\mathrm{arctan}\left(\frac{\mathrm{y}}{\mathrm{x}}\right)−\frac{\mathrm{yx}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} }\:\Rightarrow\frac{\partial^{\mathrm{2}} \mathrm{f}}{\partial\mathrm{x}^{\mathrm{2}} }\left(\mathrm{x},\mathrm{y}\right)\:=\mathrm{2arctan}\left(\frac{\mathrm{y}}{\mathrm{x}}\right) \\ $$$$+\mathrm{2x}.\frac{−\mathrm{y}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }\right)}−\mathrm{y}.\frac{\mathrm{2x}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} \right)−\mathrm{2x}.\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$=\mathrm{2arctan}\left(\frac{\mathrm{y}}{\mathrm{x}}\right)−\frac{\mathrm{2xy}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} }\:−\mathrm{y}\:.\frac{\mathrm{2xy}^{\mathrm{2}} }{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{f}_{\mathrm{xx}} =\mathrm{2arctan}\left(\frac{\mathrm{y}}{\mathrm{x}}\right)−\frac{\mathrm{2xy}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} }−\frac{\mathrm{2xy}^{\mathrm{3}} }{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$
Answered by mathmax by abdo last updated on 05/Sep/20
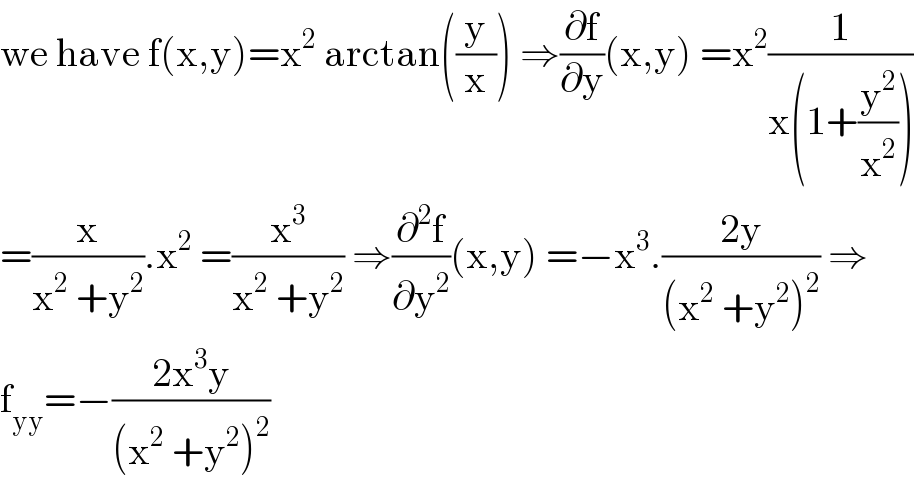
we have f(x,y)=x^2 arctan((y/x)) ⇒(∂f/∂y)(x,y) =x^2 (1/(x(1+(y^2 /x^2 )))) =(x/(x^2 +y^2 )).x^2 =(x^3 /(x^2 +y^2 )) ⇒(∂^2 f/∂y^2 )(x,y) =−x^3 .((2y)/((x^2 +y^2 )^2 )) ⇒ f_(yy) =−((2x^3 y)/((x^2 +y^2 )^2 ))
$$\mathrm{we}\:\mathrm{have}\:\mathrm{f}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{x}^{\mathrm{2}} \:\mathrm{arctan}\left(\frac{\mathrm{y}}{\mathrm{x}}\right)\:\Rightarrow\frac{\partial\mathrm{f}}{\partial\mathrm{y}}\left(\mathrm{x},\mathrm{y}\right)\:=\mathrm{x}^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{x}\left(\mathrm{1}+\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }\right)} \\ $$$$=\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} }.\mathrm{x}^{\mathrm{2}} \:=\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} }\:\Rightarrow\frac{\partial^{\mathrm{2}} \mathrm{f}}{\partial\mathrm{y}^{\mathrm{2}} }\left(\mathrm{x},\mathrm{y}\right)\:=−\mathrm{x}^{\mathrm{3}} .\frac{\mathrm{2y}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{f}_{\mathrm{yy}} =−\frac{\mathrm{2x}^{\mathrm{3}} \mathrm{y}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$
Commented by mathmax by abdo last updated on 05/Sep/20
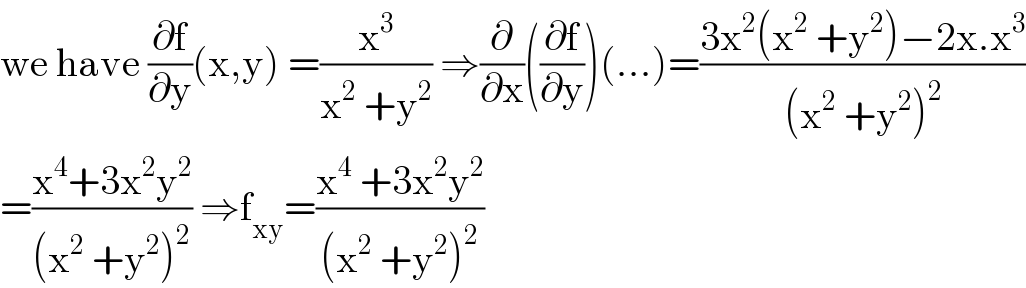
we have (∂f/∂y)(x,y) =(x^3 /(x^2 +y^2 )) ⇒(∂/∂x)((∂f/∂y))(...)=((3x^2 (x^2 +y^2 )−2x.x^3 )/((x^2 +y^2 )^2 )) =((x^4 +3x^2 y^2 )/((x^2 +y^2 )^2 )) ⇒f_(xy) =((x^4 +3x^2 y^2 )/((x^2 +y^2 )^2 ))
$$\mathrm{we}\:\mathrm{have}\:\frac{\partial\mathrm{f}}{\partial\mathrm{y}}\left(\mathrm{x},\mathrm{y}\right)\:=\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} }\:\Rightarrow\frac{\partial}{\partial\mathrm{x}}\left(\frac{\partial\mathrm{f}}{\partial\mathrm{y}}\right)\left(…\right)=\frac{\mathrm{3x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} \right)−\mathrm{2x}.\mathrm{x}^{\mathrm{3}} }{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{x}^{\mathrm{4}} +\mathrm{3x}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} }{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\Rightarrow\mathrm{f}_{\mathrm{xy}} =\frac{\mathrm{x}^{\mathrm{4}} \:+\mathrm{3x}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} }{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$
Answered by mathmax by abdo last updated on 06/Sep/20
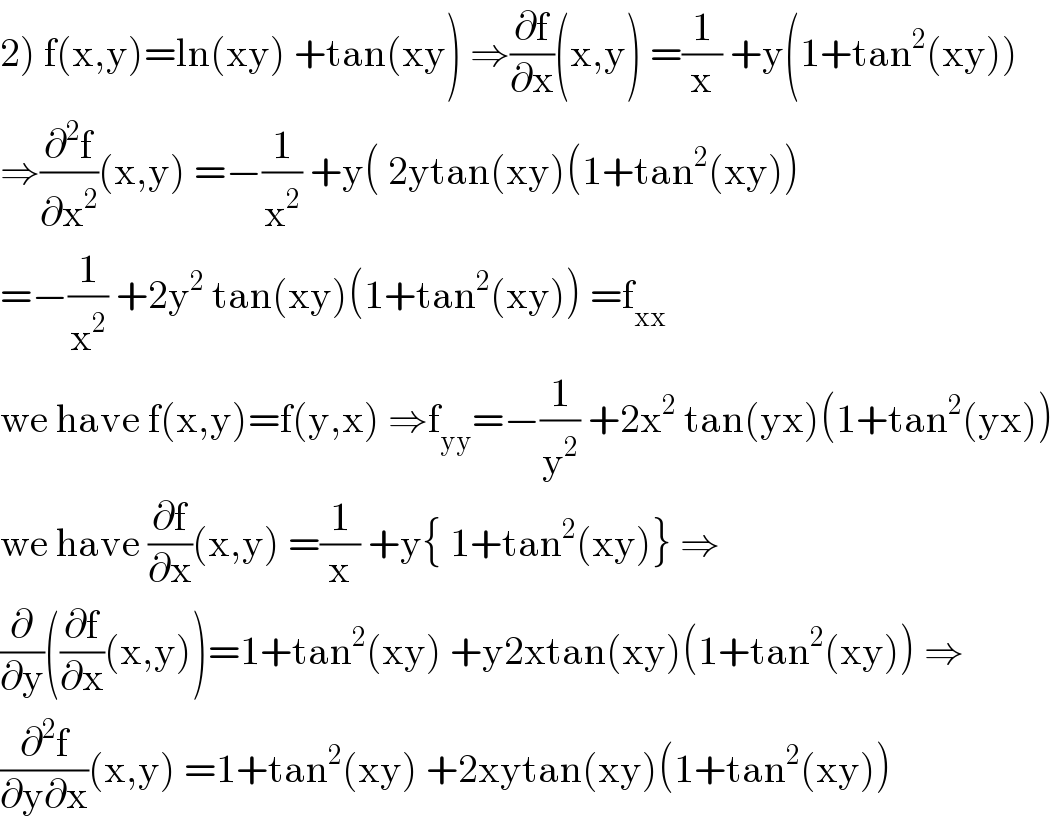
2) f(x,y)=ln(xy) +tan(xy) ⇒(∂f/∂x)(x,y) =(1/x) +y(1+tan^2 (xy)) ⇒(∂^2 f/∂x^2 )(x,y) =−(1/x^2 ) +y( 2ytan(xy)(1+tan^2 (xy)) =−(1/x^2 ) +2y^2 tan(xy)(1+tan^2 (xy)) =f_(xx) we have f(x,y)=f(y,x) ⇒f_(yy) =−(1/y^2 ) +2x^2 tan(yx)(1+tan^2 (yx)) we have (∂f/∂x)(x,y) =(1/x) +y{ 1+tan^2 (xy)} ⇒ (∂/∂y)((∂f/∂x)(x,y))=1+tan^2 (xy) +y2xtan(xy)(1+tan^2 (xy)) ⇒ (∂^2 f/(∂y∂x))(x,y) =1+tan^2 (xy) +2xytan(xy)(1+tan^2 (xy))
$$\left.\mathrm{2}\right)\:\mathrm{f}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{ln}\left(\mathrm{xy}\right)\:+\mathrm{tan}\left(\mathrm{xy}\right)\:\Rightarrow\frac{\partial\mathrm{f}}{\partial\mathrm{x}}\left(\mathrm{x},\mathrm{y}\right)\:=\frac{\mathrm{1}}{\mathrm{x}}\:+\mathrm{y}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\mathrm{xy}\right)\right) \\ $$$$\Rightarrow\frac{\partial^{\mathrm{2}} \mathrm{f}}{\partial\mathrm{x}^{\mathrm{2}} }\left(\mathrm{x},\mathrm{y}\right)\:=−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\:+\mathrm{y}\left(\:\mathrm{2ytan}\left(\mathrm{xy}\right)\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\mathrm{xy}\right)\right)\right. \\ $$$$=−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\:+\mathrm{2y}^{\mathrm{2}} \:\mathrm{tan}\left(\mathrm{xy}\right)\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\mathrm{xy}\right)\right)\:=\mathrm{f}_{\mathrm{xx}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{f}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{f}\left(\mathrm{y},\mathrm{x}\right)\:\Rightarrow\mathrm{f}_{\mathrm{yy}} =−\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{2}} }\:+\mathrm{2x}^{\mathrm{2}} \:\mathrm{tan}\left(\mathrm{yx}\right)\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\mathrm{yx}\right)\right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\frac{\partial\mathrm{f}}{\partial\mathrm{x}}\left(\mathrm{x},\mathrm{y}\right)\:=\frac{\mathrm{1}}{\mathrm{x}}\:+\mathrm{y}\left\{\:\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\mathrm{xy}\right)\right\}\:\Rightarrow \\ $$$$\frac{\partial}{\partial\mathrm{y}}\left(\frac{\partial\mathrm{f}}{\partial\mathrm{x}}\left(\mathrm{x},\mathrm{y}\right)\right)=\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\mathrm{xy}\right)\:+\mathrm{y2xtan}\left(\mathrm{xy}\right)\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\mathrm{xy}\right)\right)\:\Rightarrow \\ $$$$\frac{\partial^{\mathrm{2}} \mathrm{f}}{\partial\mathrm{y}\partial\mathrm{x}}\left(\mathrm{x},\mathrm{y}\right)\:=\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\mathrm{xy}\right)\:+\mathrm{2xytan}\left(\mathrm{xy}\right)\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\mathrm{xy}\right)\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *