Question Number 111982 by houssam last updated on 05/Sep/20

Answered by aleks041103 last updated on 05/Sep/20
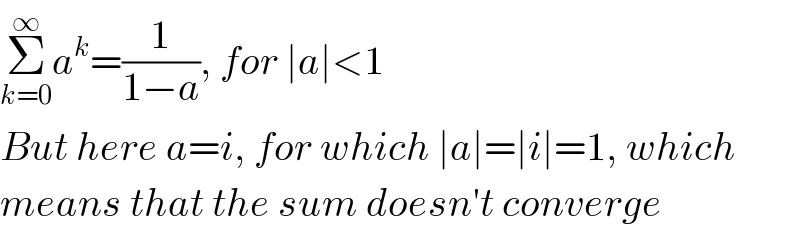
$$\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{a}^{{k}} =\frac{\mathrm{1}}{\mathrm{1}−{a}},\:{for}\:\mid{a}\mid<\mathrm{1} \\ $$$${But}\:{here}\:{a}={i},\:{for}\:{which}\:\mid{a}\mid=\mid{i}\mid=\mathrm{1},\:{which} \\ $$$${means}\:{that}\:{the}\:{sum}\:{doesn}'{t}\:{converge} \\ $$
Answered by MJS_new last updated on 05/Sep/20
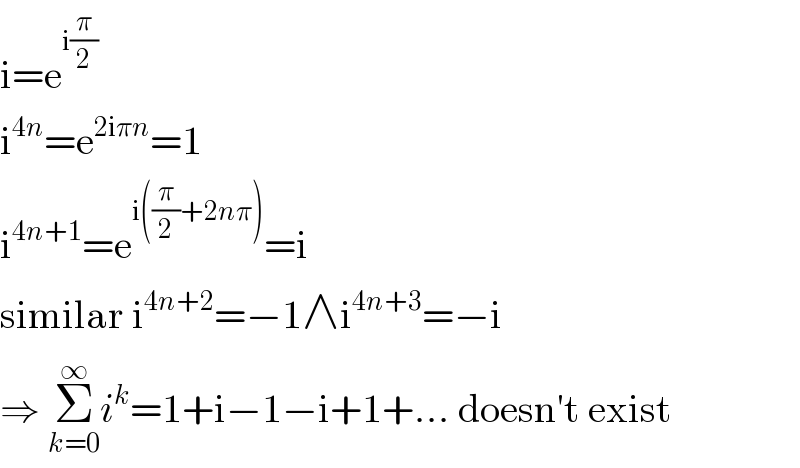
$$\mathrm{i}=\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{2}}} \\ $$$$\mathrm{i}^{\mathrm{4}{n}} =\mathrm{e}^{\mathrm{2i}\pi{n}} =\mathrm{1} \\ $$$$\mathrm{i}^{\mathrm{4}{n}+\mathrm{1}} =\mathrm{e}^{\mathrm{i}\left(\frac{\pi}{\mathrm{2}}+\mathrm{2}{n}\pi\right)} =\mathrm{i} \\ $$$$\mathrm{similar}\:\mathrm{i}^{\mathrm{4}{n}+\mathrm{2}} =−\mathrm{1}\wedge\mathrm{i}^{\mathrm{4}{n}+\mathrm{3}} =−\mathrm{i} \\ $$$$\Rightarrow\:\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{i}^{{k}} =\mathrm{1}+\mathrm{i}−\mathrm{1}−\mathrm{i}+\mathrm{1}+…\:\mathrm{doesn}'\mathrm{t}\:\mathrm{exist} \\ $$
