Question Number 111988 by ajfour last updated on 05/Sep/20
Commented by ajfour last updated on 05/Sep/20

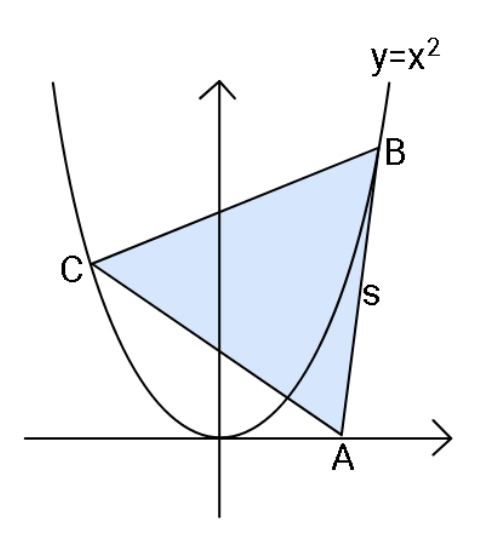
$${If}\:\bigtriangleup{ABC}\:{is}\:{equilateral}\:{with}\:{side}\:\boldsymbol{{s}}, \\ $$$${find}\:{x}-{coordinate}\:{of}\:{point}\:{A}\:{in}\: \\ $$$${terms}\:{of}\:{s}. \\ $$
Answered by mr W last updated on 06/Sep/20
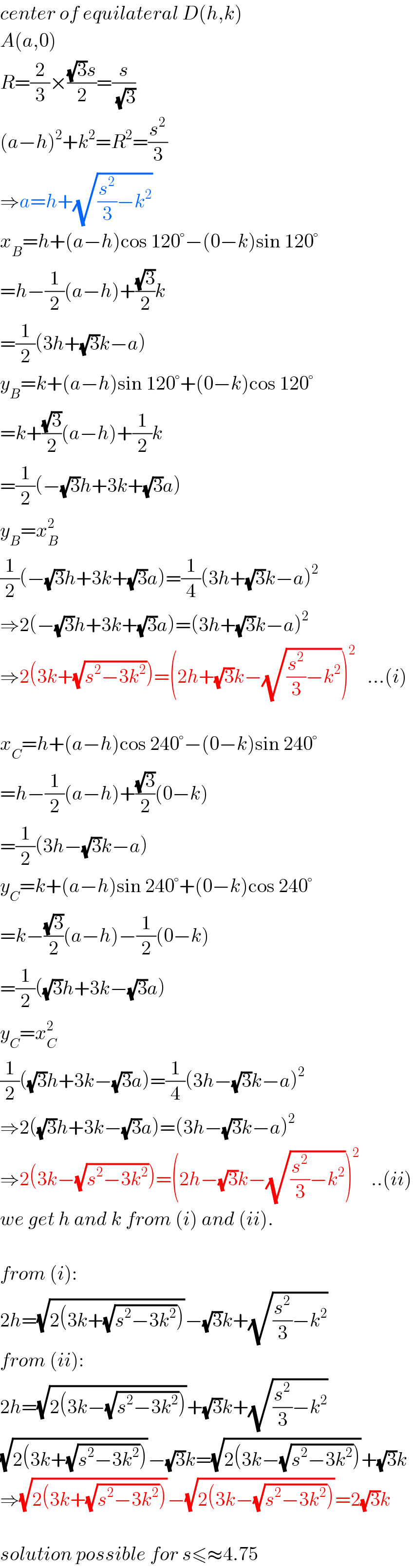
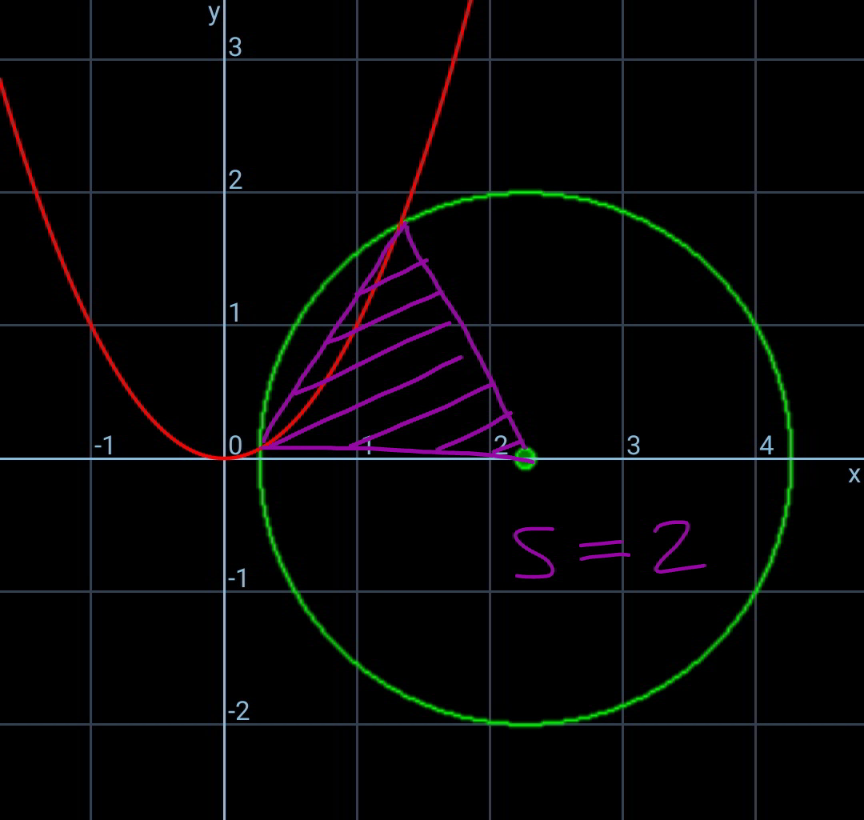
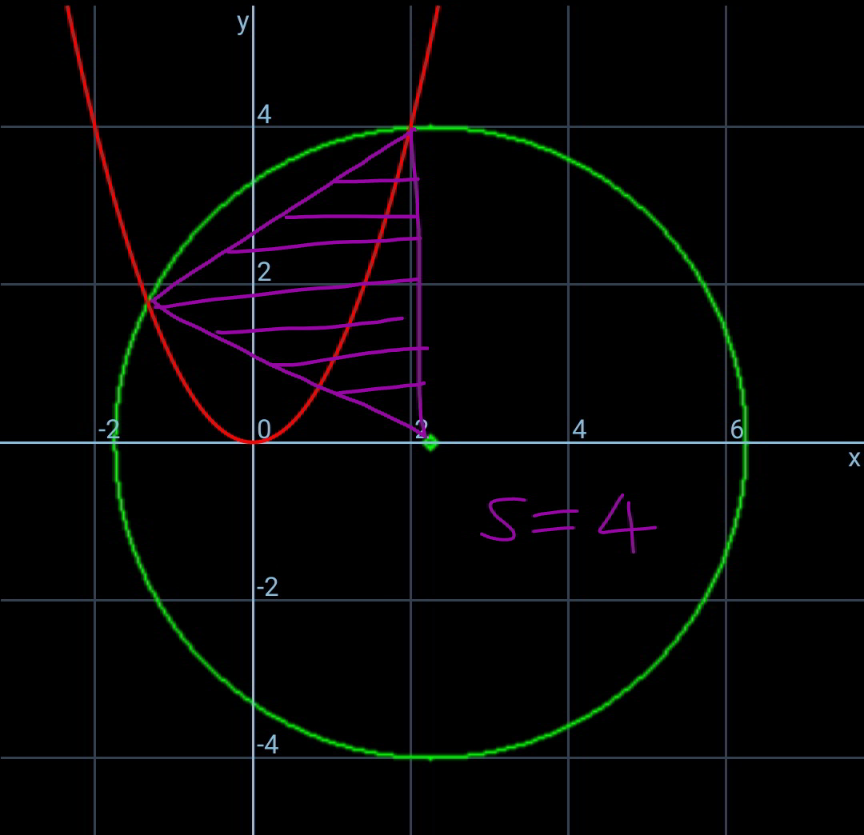
$${center}\:{of}\:{equilateral}\:{D}\left({h},{k}\right) \\ $$$${A}\left({a},\mathrm{0}\right) \\ $$$${R}=\frac{\mathrm{2}}{\mathrm{3}}×\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}}=\frac{{s}}{\:\sqrt{\mathrm{3}}} \\ $$$$\left({a}−{h}\right)^{\mathrm{2}} +{k}^{\mathrm{2}} ={R}^{\mathrm{2}} =\frac{{s}^{\mathrm{2}} }{\mathrm{3}} \\ $$$$\Rightarrow{a}={h}+\sqrt{\frac{{s}^{\mathrm{2}} }{\mathrm{3}}−{k}^{\mathrm{2}} } \\ $$$${x}_{{B}} ={h}+\left({a}−{h}\right)\mathrm{cos}\:\mathrm{120}°−\left(\mathrm{0}−{k}\right)\mathrm{sin}\:\mathrm{120}° \\ $$$$={h}−\frac{\mathrm{1}}{\mathrm{2}}\left({a}−{h}\right)+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{k} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}{h}+\sqrt{\mathrm{3}}{k}−{a}\right) \\ $$$${y}_{{B}} ={k}+\left({a}−{h}\right)\mathrm{sin}\:\mathrm{120}°+\left(\mathrm{0}−{k}\right)\mathrm{cos}\:\mathrm{120}° \\ $$$$={k}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left({a}−{h}\right)+\frac{\mathrm{1}}{\mathrm{2}}{k} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(−\sqrt{\mathrm{3}}{h}+\mathrm{3}{k}+\sqrt{\mathrm{3}}{a}\right) \\ $$$${y}_{{B}} ={x}_{{B}} ^{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(−\sqrt{\mathrm{3}}{h}+\mathrm{3}{k}+\sqrt{\mathrm{3}}{a}\right)=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{3}{h}+\sqrt{\mathrm{3}}{k}−{a}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}\left(−\sqrt{\mathrm{3}}{h}+\mathrm{3}{k}+\sqrt{\mathrm{3}}{a}\right)=\left(\mathrm{3}{h}+\sqrt{\mathrm{3}}{k}−{a}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}\left(\mathrm{3}{k}+\sqrt{{s}^{\mathrm{2}} −\mathrm{3}{k}^{\mathrm{2}} }\right)=\left(\mathrm{2}{h}+\sqrt{\mathrm{3}}{k}−\sqrt{\frac{{s}^{\mathrm{2}} }{\mathrm{3}}−{k}^{\mathrm{2}} }\right)^{\mathrm{2}} \:\:\:…\left({i}\right) \\ $$$$ \\ $$$${x}_{{C}} ={h}+\left({a}−{h}\right)\mathrm{cos}\:\mathrm{240}°−\left(\mathrm{0}−{k}\right)\mathrm{sin}\:\mathrm{240}° \\ $$$$={h}−\frac{\mathrm{1}}{\mathrm{2}}\left({a}−{h}\right)+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left(\mathrm{0}−{k}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}{h}−\sqrt{\mathrm{3}}{k}−{a}\right) \\ $$$${y}_{{C}} ={k}+\left({a}−{h}\right)\mathrm{sin}\:\mathrm{240}°+\left(\mathrm{0}−{k}\right)\mathrm{cos}\:\mathrm{240}° \\ $$$$={k}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left({a}−{h}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{0}−{k}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\mathrm{3}}{h}+\mathrm{3}{k}−\sqrt{\mathrm{3}}{a}\right) \\ $$$${y}_{{C}} ={x}_{{C}} ^{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\mathrm{3}}{h}+\mathrm{3}{k}−\sqrt{\mathrm{3}}{a}\right)=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{3}{h}−\sqrt{\mathrm{3}}{k}−{a}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}\left(\sqrt{\mathrm{3}}{h}+\mathrm{3}{k}−\sqrt{\mathrm{3}}{a}\right)=\left(\mathrm{3}{h}−\sqrt{\mathrm{3}}{k}−{a}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}\left(\mathrm{3}{k}−\sqrt{{s}^{\mathrm{2}} −\mathrm{3}{k}^{\mathrm{2}} }\right)=\left(\mathrm{2}{h}−\sqrt{\mathrm{3}}{k}−\sqrt{\frac{{s}^{\mathrm{2}} }{\mathrm{3}}−{k}^{\mathrm{2}} }\right)^{\mathrm{2}} \:\:\:..\left({ii}\right) \\ $$$${we}\:{get}\:{h}\:{and}\:{k}\:{from}\:\left({i}\right)\:{and}\:\left({ii}\right). \\ $$$$ \\ $$$${from}\:\left({i}\right): \\ $$$$\mathrm{2}{h}=\sqrt{\mathrm{2}\left(\mathrm{3}{k}+\sqrt{{s}^{\mathrm{2}} −\mathrm{3}{k}^{\mathrm{2}} }\right)}−\sqrt{\mathrm{3}}{k}+\sqrt{\frac{{s}^{\mathrm{2}} }{\mathrm{3}}−{k}^{\mathrm{2}} } \\ $$$${from}\:\left({ii}\right): \\ $$$$\mathrm{2}{h}=\sqrt{\mathrm{2}\left(\mathrm{3}{k}−\sqrt{{s}^{\mathrm{2}} −\mathrm{3}{k}^{\mathrm{2}} }\right)}+\sqrt{\mathrm{3}}{k}+\sqrt{\frac{{s}^{\mathrm{2}} }{\mathrm{3}}−{k}^{\mathrm{2}} } \\ $$$$\sqrt{\mathrm{2}\left(\mathrm{3}{k}+\sqrt{{s}^{\mathrm{2}} −\mathrm{3}{k}^{\mathrm{2}} }\right)}−\sqrt{\mathrm{3}}{k}=\sqrt{\mathrm{2}\left(\mathrm{3}{k}−\sqrt{{s}^{\mathrm{2}} −\mathrm{3}{k}^{\mathrm{2}} }\right)}+\sqrt{\mathrm{3}}{k} \\ $$$$\Rightarrow\sqrt{\mathrm{2}\left(\mathrm{3}{k}+\sqrt{{s}^{\mathrm{2}} −\mathrm{3}{k}^{\mathrm{2}} }\right)}−\sqrt{\mathrm{2}\left(\mathrm{3}{k}−\sqrt{{s}^{\mathrm{2}} −\mathrm{3}{k}^{\mathrm{2}} }\right)}=\mathrm{2}\sqrt{\mathrm{3}}{k} \\ $$$$ \\ $$$${solution}\:{possible}\:{for}\:{s}\leqslant\approx\mathrm{4}.\mathrm{75} \\ $$
Commented by mr W last updated on 06/Sep/20
Commented by mr W last updated on 06/Sep/20
Commented by mr W last updated on 06/Sep/20
Answered by ajfour last updated on 06/Sep/20

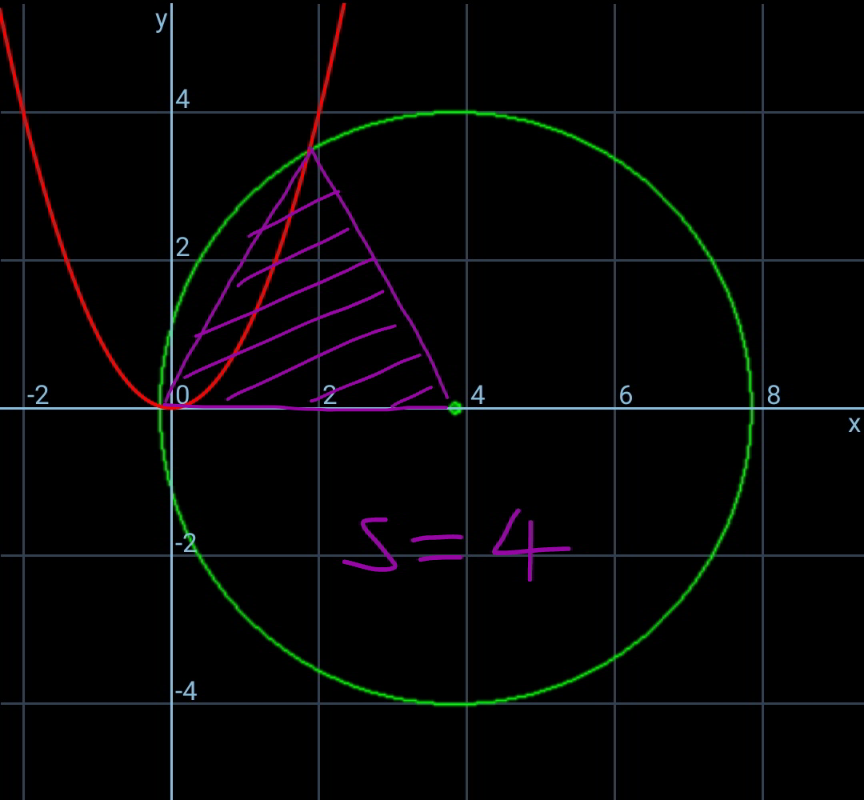
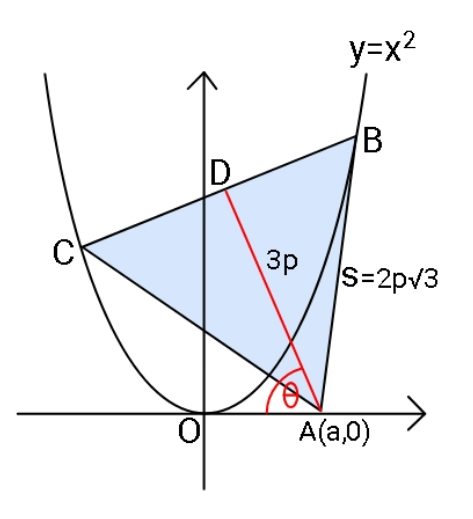
$${Let}\:\:\:{s}=\mathrm{2}{p}\sqrt{\mathrm{3}} \\ $$$${A}\left({a},\:\mathrm{0}\right) \\ $$$$\frac{{a}}{{p}}=\mathrm{3cos}\:\theta\left\{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \theta−\mathrm{tan}\:\theta\sqrt{\mathrm{tan}\:^{\mathrm{2}} \theta−\frac{\mathrm{1}}{\mathrm{3}}}\:\right\} \\ $$$${and}\:\theta\:{is}\:{obtained}\:{from} \\ $$$$\mathrm{tan}\:\theta+\sqrt{\mathrm{tan}\:^{\mathrm{2}} \theta−\frac{\mathrm{1}}{\mathrm{3}}}=\mathrm{2}{p}\mathrm{sin}\:\theta\mathrm{tan}\:\theta \\ $$$${or} \\ $$$$\frac{\mathrm{1}}{\mathrm{sin}\:^{\mathrm{2}} \theta}+\mathrm{3}\left(\mathrm{2}{p}\mathrm{sin}\:\theta−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4}\:\:\:\:\:\:\:\bigstar \\ $$
Commented by ajfour last updated on 06/Sep/20
Commented by ajfour last updated on 06/Sep/20
Commented by ajfour last updated on 06/Sep/20
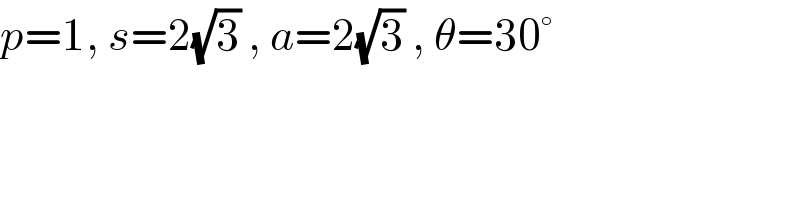
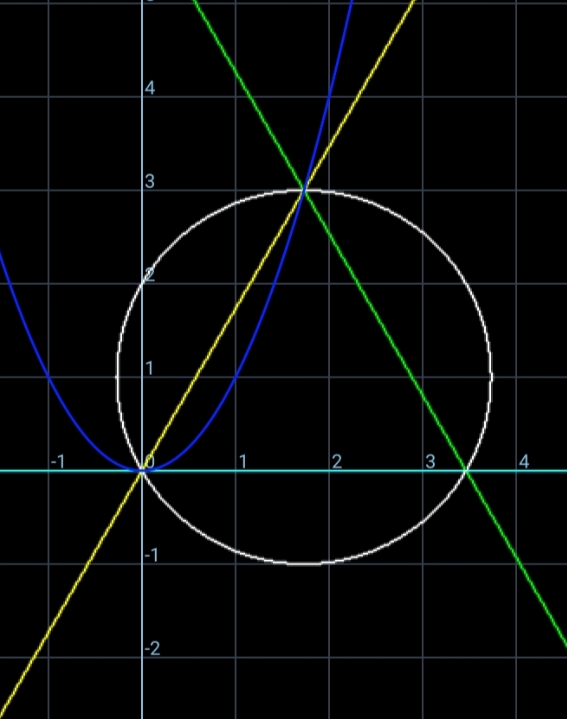
$${p}=\mathrm{1},\:{s}=\mathrm{2}\sqrt{\mathrm{3}}\:,\:{a}=\mathrm{2}\sqrt{\mathrm{3}}\:,\:\theta=\mathrm{30}° \\ $$
Commented by mr W last updated on 06/Sep/20

$${nice}\:{solution}\:{sir}! \\ $$
