Question Number 112050 by naka3546 last updated on 05/Sep/20
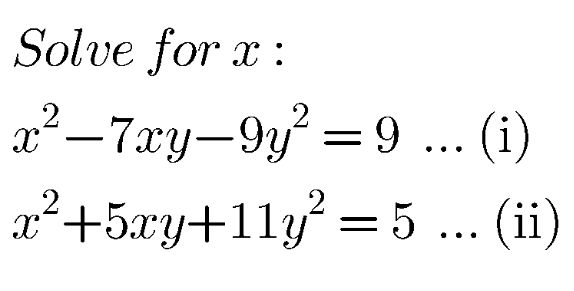
Answered by ajfour last updated on 05/Sep/20
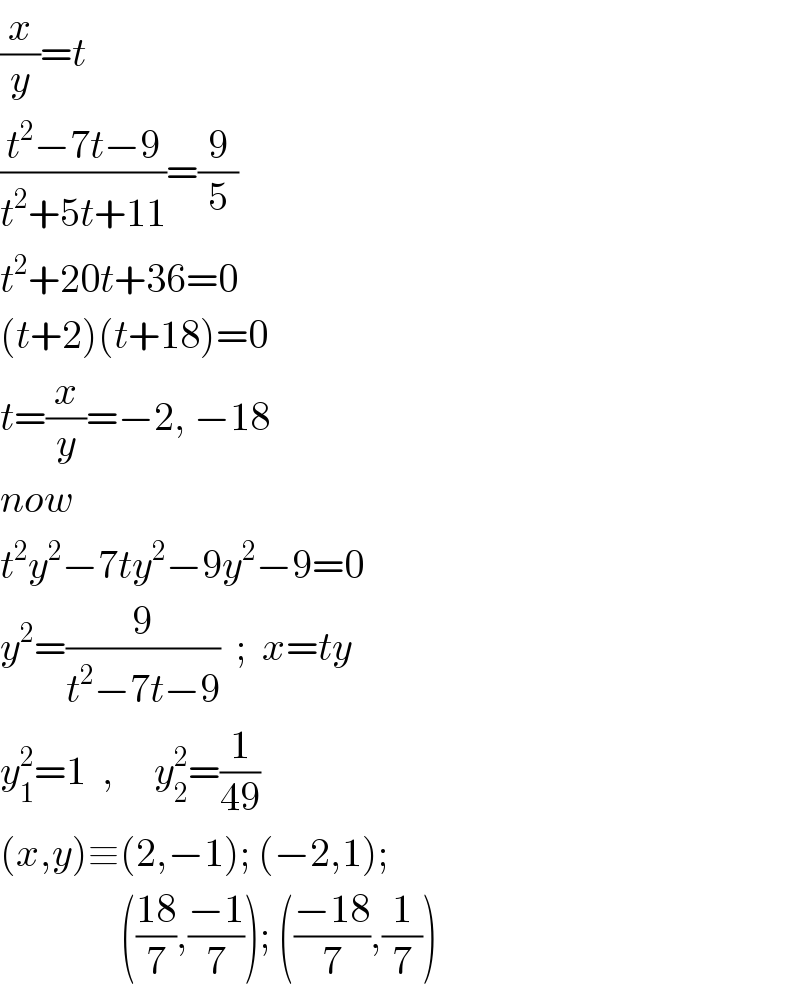
$$\frac{{x}}{{y}}={t} \\ $$$$\frac{{t}^{\mathrm{2}} −\mathrm{7}{t}−\mathrm{9}}{{t}^{\mathrm{2}} +\mathrm{5}{t}+\mathrm{11}}=\frac{\mathrm{9}}{\mathrm{5}} \\ $$$${t}^{\mathrm{2}} +\mathrm{20}{t}+\mathrm{36}=\mathrm{0} \\ $$$$\left({t}+\mathrm{2}\right)\left({t}+\mathrm{18}\right)=\mathrm{0}\:\:\: \\ $$$${t}=\frac{{x}}{{y}}=−\mathrm{2},\:−\mathrm{18} \\ $$$${now} \\ $$$${t}^{\mathrm{2}} {y}^{\mathrm{2}} −\mathrm{7}{ty}^{\mathrm{2}} −\mathrm{9}{y}^{\mathrm{2}} −\mathrm{9}=\mathrm{0} \\ $$$${y}^{\mathrm{2}} =\frac{\mathrm{9}}{{t}^{\mathrm{2}} −\mathrm{7}{t}−\mathrm{9}}\:\:;\:\:{x}={ty} \\ $$$${y}_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{1}\:\:,\:\:\:\:\:{y}_{\mathrm{2}} ^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{49}} \\ $$$$\left({x},{y}\right)\equiv\left(\mathrm{2},−\mathrm{1}\right);\:\left(−\mathrm{2},\mathrm{1}\right);\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\frac{\mathrm{18}}{\mathrm{7}},\frac{−\mathrm{1}}{\mathrm{7}}\right);\:\left(\frac{−\mathrm{18}}{\mathrm{7}},\frac{\mathrm{1}}{\mathrm{7}}\right)\: \\ $$
Answered by MJS_new last updated on 05/Sep/20
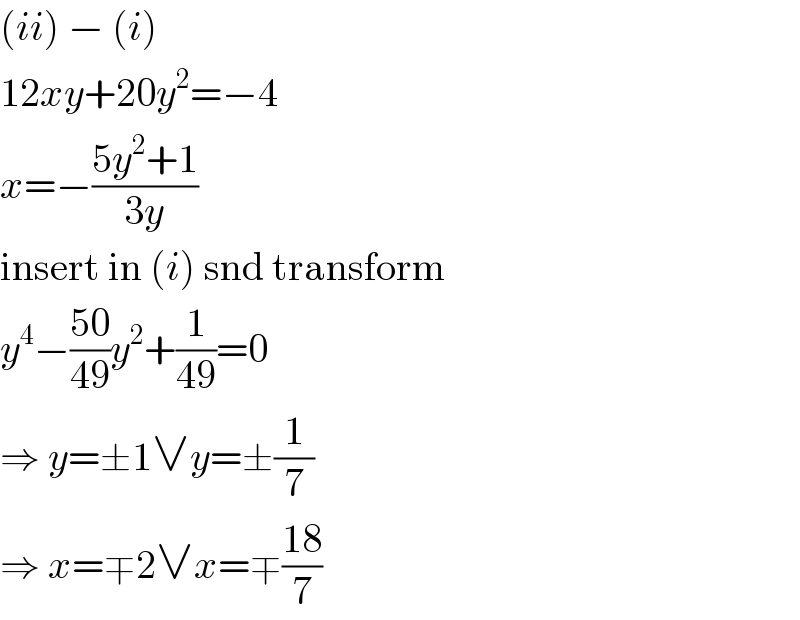
$$\left({ii}\right)\:−\:\left({i}\right) \\ $$$$\mathrm{12}{xy}+\mathrm{20}{y}^{\mathrm{2}} =−\mathrm{4} \\ $$$${x}=−\frac{\mathrm{5}{y}^{\mathrm{2}} +\mathrm{1}}{\mathrm{3}{y}} \\ $$$$\mathrm{insert}\:\mathrm{in}\:\left({i}\right)\:\mathrm{snd}\:\mathrm{transform} \\ $$$${y}^{\mathrm{4}} −\frac{\mathrm{50}}{\mathrm{49}}{y}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{49}}=\mathrm{0} \\ $$$$\Rightarrow\:{y}=\pm\mathrm{1}\vee{y}=\pm\frac{\mathrm{1}}{\mathrm{7}} \\ $$$$\Rightarrow\:{x}=\mp\mathrm{2}\vee{x}=\mp\frac{\mathrm{18}}{\mathrm{7}} \\ $$
Answered by 1549442205PVT last updated on 06/Sep/20

$$\left.\mathrm{F}\left.\mathrm{rom}\:\mathrm{i}\right)\mathrm{and}\:\mathrm{ii}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{5}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{7xy}−\mathrm{9y}^{\mathrm{2}} \right)=\mathrm{9}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{5xy}+\mathrm{11y}^{\mathrm{2}} \right) \\ $$$$\Leftrightarrow\mathrm{4x}^{\mathrm{2}} +\mathrm{80xy}+\mathrm{144y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{20xy}+\mathrm{36y}^{\mathrm{2}} =\mathrm{0}\Leftrightarrow\left(\left(\mathrm{x}+\mathrm{2y}\right)\left(\mathrm{x}+\mathrm{18y}\right)=\mathrm{0}\right. \\ $$$$\left.\mathrm{i}\right)\mathrm{x}+\mathrm{2y}=\mathrm{0}\Leftrightarrow\mathrm{x}=−\mathrm{2y}.\mathrm{Replace}\:\mathrm{into}\:\left(\mathrm{i}\right) \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{4y}^{\mathrm{2}} +\mathrm{14y}^{\mathrm{2}} −\mathrm{9y}^{\mathrm{2}} =\mathrm{9} \\ $$$$\Leftrightarrow\mathrm{y}^{\mathrm{2}} =\mathrm{1}\Leftrightarrow\mathrm{y}=\pm\mathrm{1}\Rightarrow\mathrm{x}=\mp\mathrm{2} \\ $$$$\left.\mathrm{ii}\right)\mathrm{x}+\mathrm{18y}=\mathrm{0}\Leftrightarrow\mathrm{x}=−\mathrm{18y}.\mathrm{Replace}\:\mathrm{into} \\ $$$$\left(\mathrm{i}\right)\mathrm{we}\:\mathrm{get}\:\mathrm{324y}^{\mathrm{2}} +\mathrm{126y}^{\mathrm{2}} −\mathrm{9y}^{\mathrm{2}} =\mathrm{9} \\ $$$$\Leftrightarrow\mathrm{441y}^{\mathrm{2}} =\mathrm{9}\Leftrightarrow\mathrm{y}^{\mathrm{2}} =\frac{\mathrm{9}}{\mathrm{441}}\Leftrightarrow\mathrm{y}=\pm\frac{\mathrm{1}}{\mathrm{7}} \\ $$$$\Rightarrow\mathrm{x}=\mp\frac{\mathrm{18}}{\mathrm{7}}.\mathrm{Thus}\:\mathrm{the}\:\mathrm{given}\:\mathrm{system}\:\mathrm{has} \\ $$$$\mathrm{four}\:\mathrm{roots} \\ $$$$\left(\boldsymbol{\mathrm{x}},\boldsymbol{\mathrm{y}}\right)\in\left\{\left(\mathrm{1},−\mathrm{2}\right),\left(−\mathrm{1},\mathrm{2}\right),\left(\frac{\mathrm{1}}{\mathrm{7}},−\frac{\mathrm{18}}{\mathrm{7}}\right),\left(\frac{−\mathrm{1}}{\mathrm{7}},\frac{\mathrm{18}}{\mathrm{7}}\right)\right\} \\ $$
