Question Number 112058 by mohssinee last updated on 05/Sep/20

Answered by MJS_new last updated on 06/Sep/20
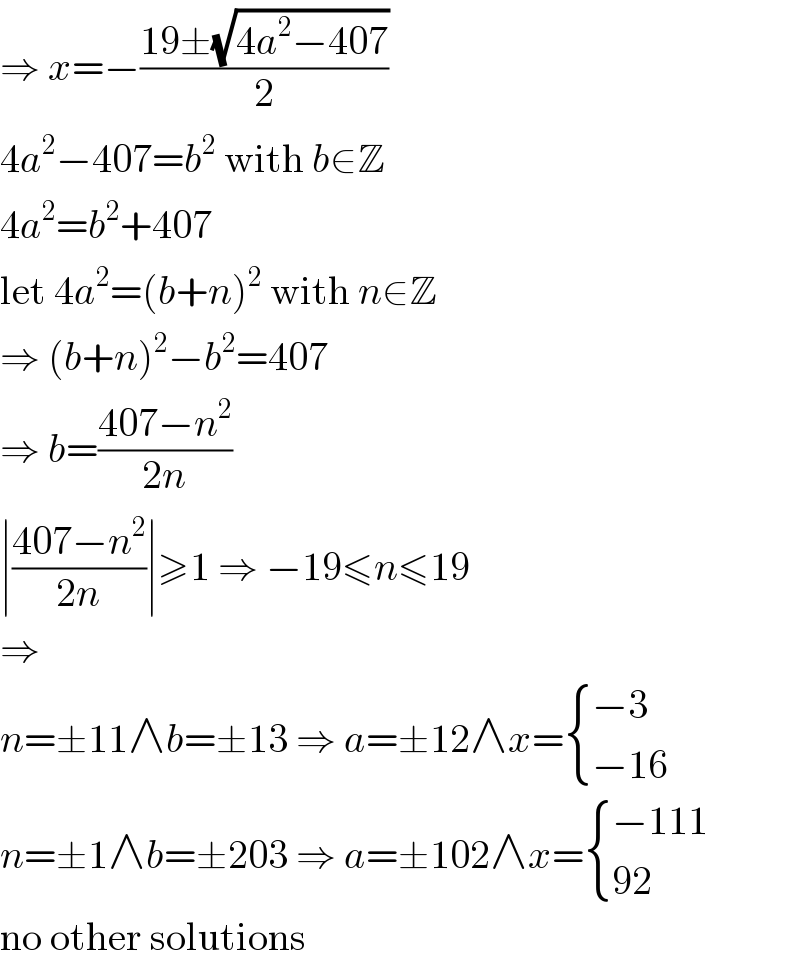
$$\Rightarrow\:{x}=−\frac{\mathrm{19}\pm\sqrt{\mathrm{4}{a}^{\mathrm{2}} −\mathrm{407}}}{\mathrm{2}} \\ $$$$\mathrm{4}{a}^{\mathrm{2}} −\mathrm{407}={b}^{\mathrm{2}} \:\mathrm{with}\:{b}\in\mathbb{Z} \\ $$$$\mathrm{4}{a}^{\mathrm{2}} ={b}^{\mathrm{2}} +\mathrm{407} \\ $$$$\mathrm{let}\:\mathrm{4}{a}^{\mathrm{2}} =\left({b}+{n}\right)^{\mathrm{2}} \:\mathrm{with}\:{n}\in\mathbb{Z} \\ $$$$\Rightarrow\:\left({b}+{n}\right)^{\mathrm{2}} −{b}^{\mathrm{2}} =\mathrm{407} \\ $$$$\Rightarrow\:{b}=\frac{\mathrm{407}−{n}^{\mathrm{2}} }{\mathrm{2}{n}} \\ $$$$\mid\frac{\mathrm{407}−{n}^{\mathrm{2}} }{\mathrm{2}{n}}\mid\geqslant\mathrm{1}\:\Rightarrow\:−\mathrm{19}\leqslant{n}\leqslant\mathrm{19} \\ $$$$\Rightarrow \\ $$$${n}=\pm\mathrm{11}\wedge{b}=\pm\mathrm{13}\:\Rightarrow\:{a}=\pm\mathrm{12}\wedge{x}=\begin{cases}{−\mathrm{3}}\\{−\mathrm{16}}\end{cases} \\ $$$${n}=\pm\mathrm{1}\wedge{b}=\pm\mathrm{203}\:\Rightarrow\:{a}=\pm\mathrm{102}\wedge{x}=\begin{cases}{−\mathrm{111}}\\{\mathrm{92}}\end{cases} \\ $$$$\mathrm{no}\:\mathrm{other}\:\mathrm{solutions} \\ $$
