Question Number 112128 by mohammad17 last updated on 06/Sep/20

Commented by mohammad17 last updated on 06/Sep/20
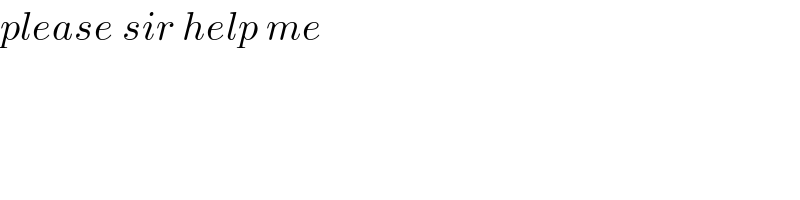
$${please}\:{sir}\:{help}\:{me} \\ $$
Commented by bobhans last updated on 06/Sep/20
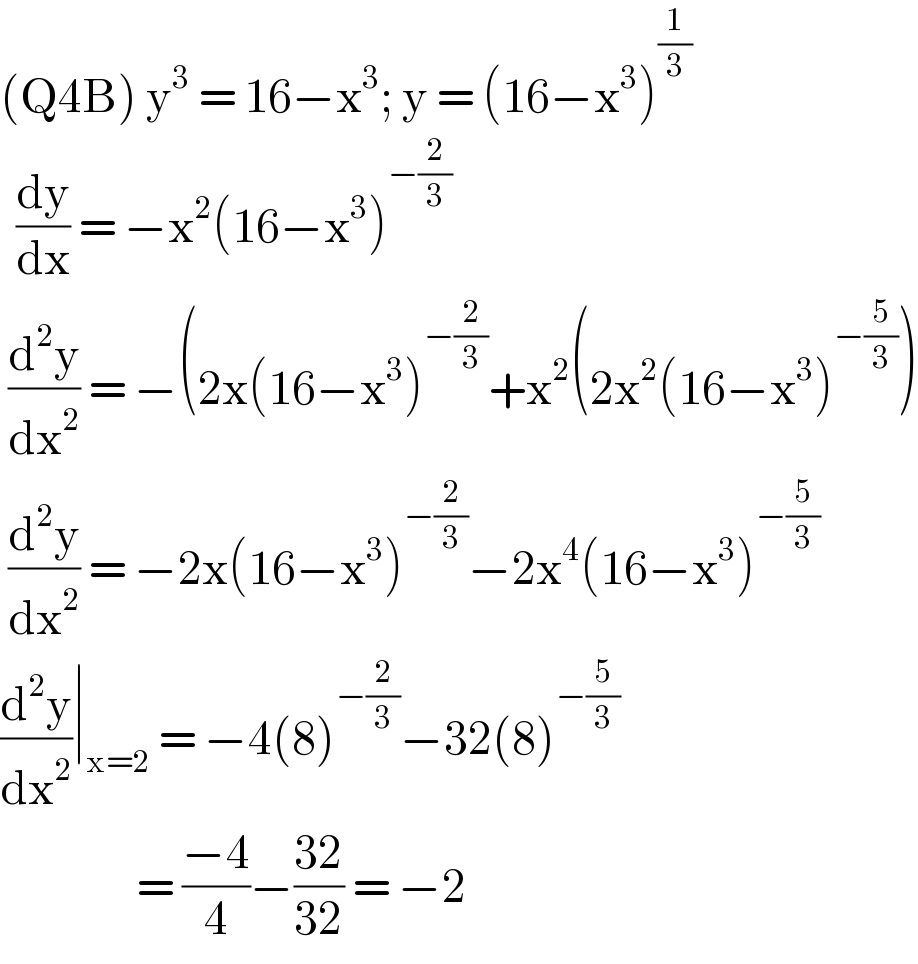
$$\left(\mathrm{Q4B}\right)\:\mathrm{y}^{\mathrm{3}} \:=\:\mathrm{16}−\mathrm{x}^{\mathrm{3}} ;\:\mathrm{y}\:=\:\left(\mathrm{16}−\mathrm{x}^{\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\:\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:−\mathrm{x}^{\mathrm{2}} \left(\mathrm{16}−\mathrm{x}^{\mathrm{3}} \right)^{−\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$$\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:=\:−\left(\mathrm{2x}\left(\mathrm{16}−\mathrm{x}^{\mathrm{3}} \right)^{−\frac{\mathrm{2}}{\mathrm{3}}} +\mathrm{x}^{\mathrm{2}} \left(\mathrm{2x}^{\mathrm{2}} \left(\mathrm{16}−\mathrm{x}^{\mathrm{3}} \right)^{−\frac{\mathrm{5}}{\mathrm{3}}} \right)\right. \\ $$$$\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:=\:−\mathrm{2x}\left(\mathrm{16}−\mathrm{x}^{\mathrm{3}} \right)^{−\frac{\mathrm{2}}{\mathrm{3}}} −\mathrm{2x}^{\mathrm{4}} \left(\mathrm{16}−\mathrm{x}^{\mathrm{3}} \right)^{−\frac{\mathrm{5}}{\mathrm{3}}} \\ $$$$\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\mid_{\mathrm{x}=\mathrm{2}} \:=\:−\mathrm{4}\left(\mathrm{8}\right)^{−\frac{\mathrm{2}}{\mathrm{3}}} −\mathrm{32}\left(\mathrm{8}\right)^{−\frac{\mathrm{5}}{\mathrm{3}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{−\mathrm{4}}{\mathrm{4}}−\frac{\mathrm{32}}{\mathrm{32}}\:=\:−\mathrm{2}\: \\ $$
Answered by bemath last updated on 06/Sep/20

$$\left({Q}\mathrm{1}\right)\:{y}−{xy}\:=\:\mathrm{2}{x},\:{y}\:=\:\frac{\mathrm{2}{x}}{−{x}+\mathrm{1}} \\ $$$$\Rightarrow\:{y}'=\frac{\mathrm{2}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:,\:{m}_{{normal}\:} =−\frac{\mathrm{1}}{{y}'} \\ $$$${m}_{{normal}} =−\frac{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }{\mathrm{2}}\:{parallel}\:{to} \\ $$$${line}\:\mathrm{2}{x}+{y}=\mathrm{0}\:\Rightarrow\:−\frac{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }{\mathrm{2}}\:=\:−\mathrm{2} \\ $$$$\Rightarrow\left(\mathrm{1}−{x}\right)^{\mathrm{2}} =\:\mathrm{4}\:\rightarrow\begin{cases}{\mathrm{1}−{x}=\mathrm{2},\:{x}=−\mathrm{1}}\\{\mathrm{1}−{x}=−\mathrm{2},{x}=\mathrm{3}}\end{cases} \\ $$$${for}\:\begin{cases}{{x}=−\mathrm{1},\:{y}=\frac{−\mathrm{2}}{\mathrm{2}}=−\mathrm{1}}\\{{x}=\mathrm{3},{y}=\frac{\mathrm{6}}{−\mathrm{2}}=−\mathrm{3}}\end{cases} \\ $$$$\rightarrow\begin{cases}{{normal}\:{at}\:{point}\left(−\mathrm{1},−\mathrm{1}\right)\:{is}\:\mathrm{2}{x}+{y}=−\mathrm{3}}\\{{normal}\:{at}\:{point}\left(\mathrm{3},−\mathrm{3}\right)\:{is}\:\mathrm{2}{x}+{y}=\mathrm{3}}\end{cases} \\ $$
Commented by mohammad17 last updated on 06/Sep/20
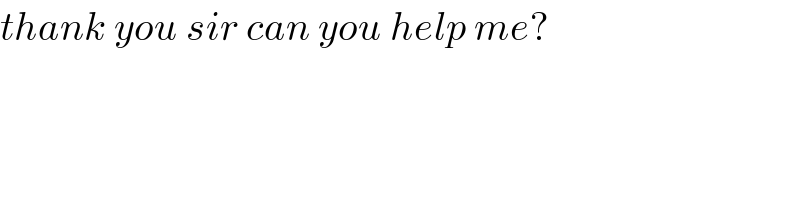
$${thank}\:{you}\:{sir}\:{can}\:{you}\:{help}\:{me}? \\ $$
Commented by bemath last updated on 06/Sep/20

$${ok} \\ $$
Answered by bemath last updated on 06/Sep/20
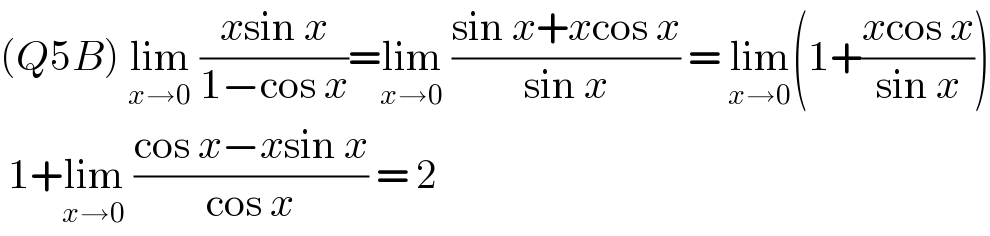
$$\left({Q}\mathrm{5}{B}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}\mathrm{sin}\:{x}}{\mathrm{1}−\mathrm{cos}\:{x}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:{x}+{x}\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+\frac{{x}\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}}\right) \\ $$$$\:\mathrm{1}+\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:{x}−{x}\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}}\:=\:\mathrm{2} \\ $$
Answered by bemath last updated on 06/Sep/20
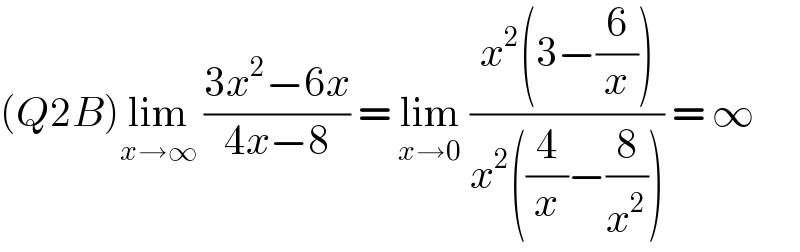
$$\left({Q}\mathrm{2}{B}\right)\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{6}{x}}{\mathrm{4}{x}−\mathrm{8}}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} \left(\mathrm{3}−\frac{\mathrm{6}}{{x}}\right)}{{x}^{\mathrm{2}} \left(\frac{\mathrm{4}}{{x}}−\frac{\mathrm{8}}{{x}^{\mathrm{2}} }\right)}\:=\:\infty \\ $$
Answered by mathmax by abdo last updated on 06/Sep/20

$$\left.\mathrm{Q}_{\mathrm{3}} \right)\:\:\:\mathrm{y}\left(\mathrm{x}\right)=\frac{\mathrm{x}^{\mathrm{3}} −\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:\:\:\mathrm{y}\:\mathrm{is}\:\mathrm{not}\:\mathrm{conutinue}\:\mathrm{at}\:\mathrm{x}_{\mathrm{0}} =\mathrm{1}\:\mathrm{but}\: \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}} \:\mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}} \:\:\frac{\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)}{\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{1}\right)}\:=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}} \:\:\:\frac{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}}{\mathrm{x}+\mathrm{1}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\mathrm{but}\:\mathrm{if}\:\mathrm{we}\:\mathrm{put}\:\begin{cases}{\mathrm{y}\left(\mathrm{x}\right)=\frac{\mathrm{x}^{\mathrm{3}} −\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:\mathrm{if}\:\mathrm{x}\neq\mathrm{1}}\\{\mathrm{y}\left(\mathrm{1}\right)=\frac{\mathrm{3}}{\mathrm{2}}}\end{cases} \\ $$$$\mathrm{this}\:\mathrm{function}\:\mathrm{become}\:\mathrm{continue}\:\mathrm{on}\:\mathrm{R} \\ $$$$\left.\mathrm{2}\right)\:\mathrm{y}\left(\mathrm{x}\right)=\frac{\mid\mathrm{x}\mid}{\mathrm{x}}\:\:\:\:\:\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}^{+} } \:\:\mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}^{+} } \:\:\frac{\mathrm{x}}{\mathrm{x}}\:=\mathrm{1}\:\:\left(\mathrm{continue}\:\mathrm{at}\:\mathrm{right}\right) \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}^{−} } \:\:\:\mathrm{y}\left(\mathrm{x}\right)=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}^{−} } \:\:\frac{−\mathrm{x}}{\mathrm{x}}\:=−\mathrm{1}\:\:\:\left(\mathrm{continue}\:\mathrm{at}\:\mathrm{left}\right) \\ $$$$\mathrm{but}\:\mathrm{y}\:\mathrm{is}\:\mathrm{not}\:\mathrm{continue}\:\mathrm{at} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 06/Sep/20

$$\mathrm{at}\:\mathrm{0} \\ $$
Answered by mathmax by abdo last updated on 06/Sep/20
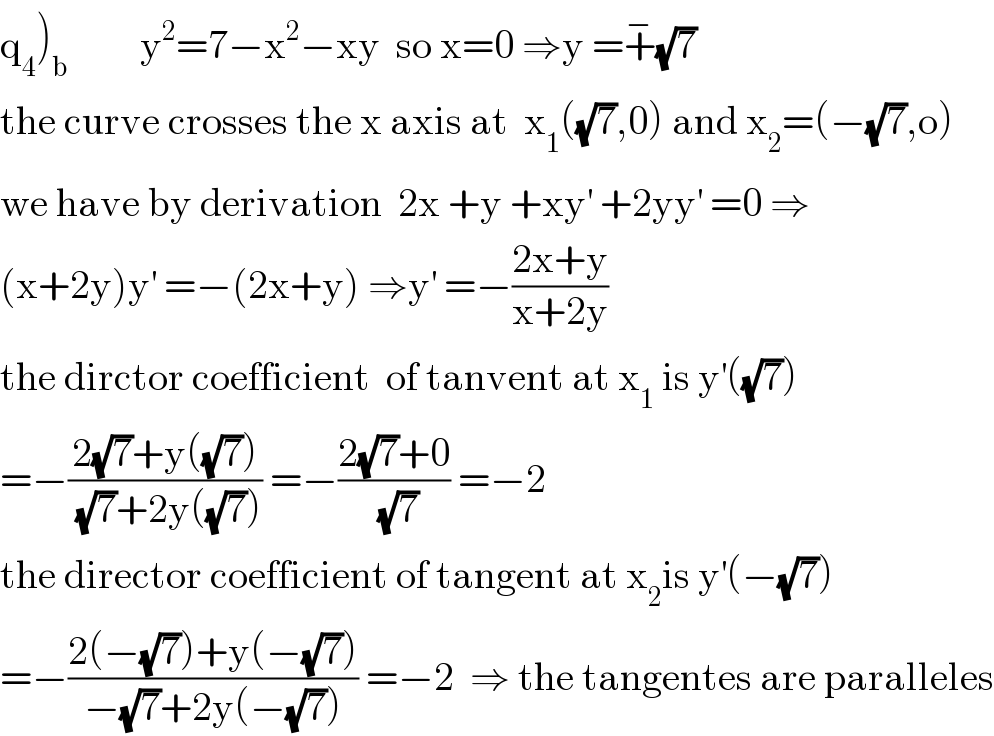
$$\left.\mathrm{q}_{\mathrm{4}} \right)_{\mathrm{b}} \:\:\:\:\:\:\:\:\:\mathrm{y}^{\mathrm{2}} =\mathrm{7}−\mathrm{x}^{\mathrm{2}} −\mathrm{xy}\:\:\mathrm{so}\:\mathrm{x}=\mathrm{0}\:\Rightarrow\mathrm{y}\:=\overset{−} {+}\sqrt{\mathrm{7}} \\ $$$$\mathrm{the}\:\mathrm{curve}\:\mathrm{crosses}\:\mathrm{the}\:\mathrm{x}\:\mathrm{axis}\:\mathrm{at}\:\:\mathrm{x}_{\mathrm{1}} \left(\sqrt{\mathrm{7}},\mathrm{0}\right)\:\mathrm{and}\:\mathrm{x}_{\mathrm{2}} =\left(−\sqrt{\mathrm{7}},\mathrm{o}\right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{by}\:\mathrm{derivation}\:\:\mathrm{2x}\:+\mathrm{y}\:+\mathrm{xy}^{'} \:+\mathrm{2yy}^{'} \:=\mathrm{0}\:\Rightarrow \\ $$$$\left(\mathrm{x}+\mathrm{2y}\right)\mathrm{y}^{'} \:=−\left(\mathrm{2x}+\mathrm{y}\right)\:\Rightarrow\mathrm{y}^{'} \:=−\frac{\mathrm{2x}+\mathrm{y}}{\mathrm{x}+\mathrm{2y}} \\ $$$$\mathrm{the}\:\mathrm{dirctor}\:\mathrm{coefficient}\:\:\mathrm{of}\:\mathrm{tanvent}\:\mathrm{at}\:\mathrm{x}_{\mathrm{1}} \:\mathrm{is}\:\mathrm{y}^{'} \left(\sqrt{\mathrm{7}}\right) \\ $$$$=−\frac{\mathrm{2}\sqrt{\mathrm{7}}+\mathrm{y}\left(\sqrt{\mathrm{7}}\right)}{\:\sqrt{\mathrm{7}}+\mathrm{2y}\left(\sqrt{\mathrm{7}}\right)}\:=−\frac{\mathrm{2}\sqrt{\mathrm{7}}+\mathrm{0}}{\:\sqrt{\mathrm{7}}}\:=−\mathrm{2} \\ $$$$\mathrm{the}\:\mathrm{director}\:\mathrm{coefficient}\:\mathrm{of}\:\mathrm{tangent}\:\mathrm{at}\:\mathrm{x}_{\mathrm{2}} \mathrm{is}\:\mathrm{y}^{'} \left(−\sqrt{\mathrm{7}}\right) \\ $$$$=−\frac{\mathrm{2}\left(−\sqrt{\mathrm{7}}\right)+\mathrm{y}\left(−\sqrt{\mathrm{7}}\right)}{−\sqrt{\mathrm{7}}+\mathrm{2y}\left(−\sqrt{\mathrm{7}}\right)}\:=−\mathrm{2}\:\:\Rightarrow\:\mathrm{the}\:\mathrm{tangentes}\:\mathrm{are}\:\mathrm{paralleles} \\ $$
