Question Number 112208 by Khalmohmmad last updated on 06/Sep/20
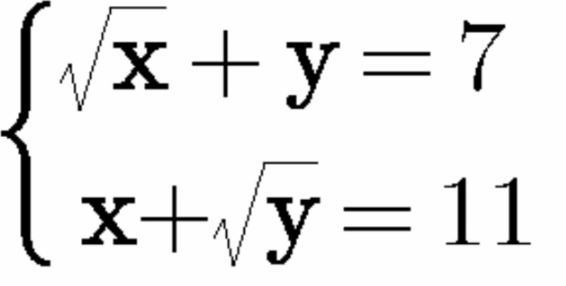
Commented by Dwaipayan Shikari last updated on 06/Sep/20
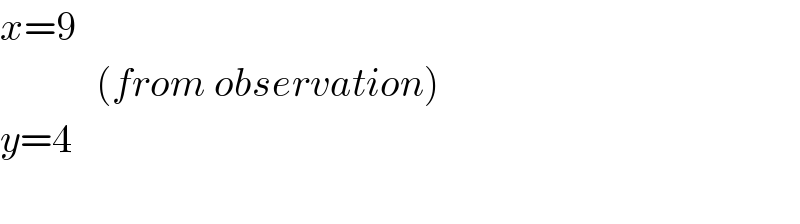
$${x}=\mathrm{9} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\left({from}\:{observation}\right) \\ $$$${y}=\mathrm{4} \\ $$$$ \\ $$
Commented by Khalmohmmad last updated on 06/Sep/20
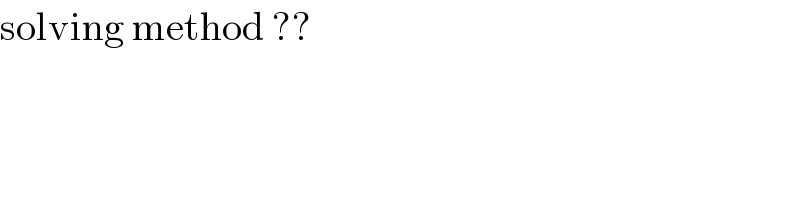
$$\mathrm{solving}\:\mathrm{method}\:?? \\ $$
Commented by Dwaipayan Shikari last updated on 06/Sep/20
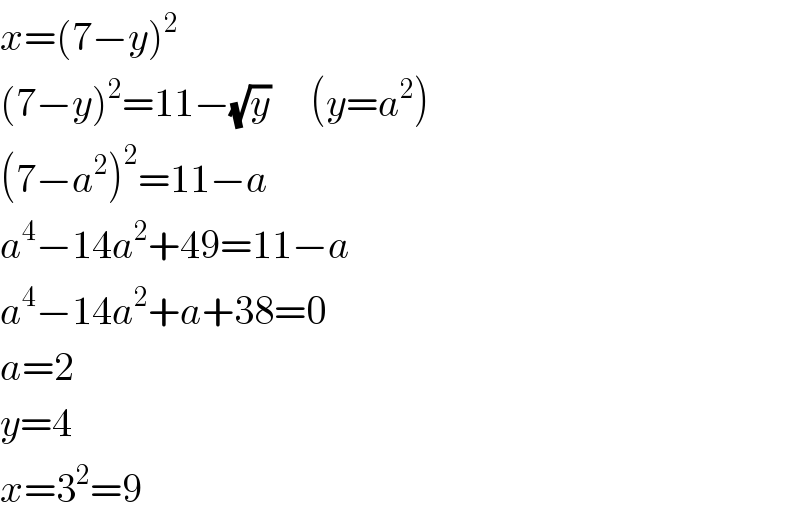
$${x}=\left(\mathrm{7}−{y}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{7}−{y}\right)^{\mathrm{2}} =\mathrm{11}−\sqrt{{y}}\:\:\:\:\:\left({y}={a}^{\mathrm{2}} \right) \\ $$$$\left(\mathrm{7}−{a}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{11}−{a} \\ $$$${a}^{\mathrm{4}} −\mathrm{14}{a}^{\mathrm{2}} +\mathrm{49}=\mathrm{11}−{a} \\ $$$${a}^{\mathrm{4}} −\mathrm{14}{a}^{\mathrm{2}} +{a}+\mathrm{38}=\mathrm{0} \\ $$$${a}=\mathrm{2} \\ $$$${y}=\mathrm{4} \\ $$$${x}=\mathrm{3}^{\mathrm{2}} =\mathrm{9} \\ $$
Answered by bemath last updated on 07/Sep/20
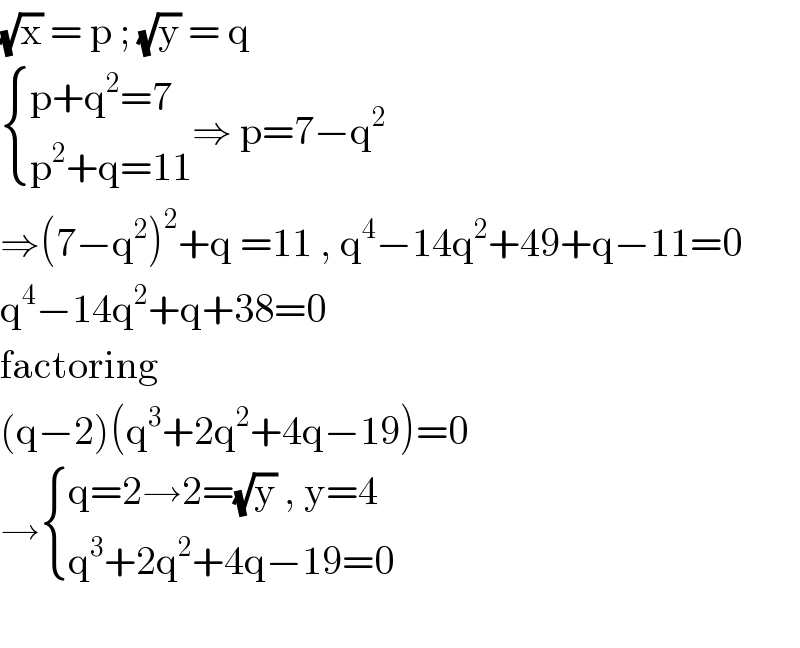
$$\sqrt{\mathrm{x}}\:=\:\mathrm{p}\:;\:\sqrt{\mathrm{y}}\:=\:\mathrm{q} \\ $$$$\begin{cases}{\mathrm{p}+\mathrm{q}^{\mathrm{2}} =\mathrm{7}}\\{\mathrm{p}^{\mathrm{2}} +\mathrm{q}=\mathrm{11}}\end{cases}\Rightarrow\:\mathrm{p}=\mathrm{7}−\mathrm{q}^{\mathrm{2}} \\ $$$$\Rightarrow\left(\mathrm{7}−\mathrm{q}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{q}\:=\mathrm{11}\:,\:\mathrm{q}^{\mathrm{4}} −\mathrm{14q}^{\mathrm{2}} +\mathrm{49}+\mathrm{q}−\mathrm{11}=\mathrm{0} \\ $$$$\mathrm{q}^{\mathrm{4}} −\mathrm{14q}^{\mathrm{2}} +\mathrm{q}+\mathrm{38}=\mathrm{0} \\ $$$$\mathrm{factoring}\: \\ $$$$\left(\mathrm{q}−\mathrm{2}\right)\left(\mathrm{q}^{\mathrm{3}} +\mathrm{2q}^{\mathrm{2}} +\mathrm{4q}−\mathrm{19}\right)=\mathrm{0} \\ $$$$\rightarrow\begin{cases}{\mathrm{q}=\mathrm{2}\rightarrow\mathrm{2}=\sqrt{\mathrm{y}}\:,\:\mathrm{y}=\mathrm{4}}\\{\mathrm{q}^{\mathrm{3}} +\mathrm{2q}^{\mathrm{2}} +\mathrm{4q}−\mathrm{19}=\mathrm{0}}\end{cases} \\ $$$$ \\ $$
