Question-112366

Question Number 112366 by mathdave last updated on 07/Sep/20

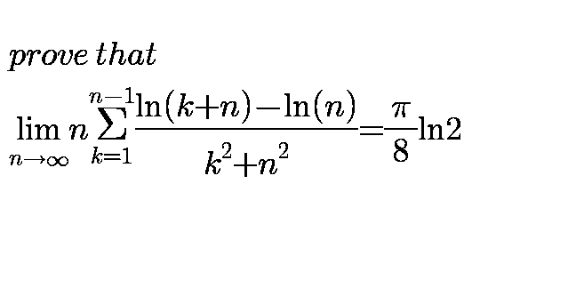
Answered by mathmax by abdo last updated on 07/Sep/20

let S_n =n Σ_(k=1) ^(n−1) ((ln(k+n)−ln(n))/(n^2 +k^2 )) ⇒ S_n =(1/n) Σ_(k=1) ^(n−1) ((ln(((n+k)/n)))/(1+(k^2 /n^2 ))) =(1/n) Σ_(k=1) ^(n−1) ((ln(1+(k/n)))/(1+((k/n))^2 )) so S_n is a Rieman sum and lim_(n→+∞) S_n =∫_0 ^1 ((ln(1+x))/(1+x^2 )) dx changement x=tant give ∫_0 ^1 ((ln(1+x))/(1+x^2 ))dx =∫_0 ^(π/4) ((ln(1+tant))/(1+tan^2 t))(1+tan^2 t)dt =∫_0 ^(π/4) ln(1+tan(t))dt =_(t=(π/4)−u) ∫_0 ^(π/4) ln(1+tan((π/4)−u))du =∫_0 ^(π/4) ln(1+((1−tanu)/(1+tanu)))du =∫_0 ^(π/4) ln((2/(1+tanu)))du =(π/4)ln(2)−∫_0 ^(π/4) ln(1+tanu)du ⇒ 2∫_0 ^(π/4) ln(1+tanu)du =(π/4)ln(2) ⇒∫_0 ^(π/4) ln(1+tanu)du =(π/8)ln(2) =∫_0 ^1 ((ln(1+x))/(1+x^2 ))dx =lim_(n→+∞) S_n

$$\mathrm{let}\:\mathrm{S}_{\mathrm{n}} =\mathrm{n}\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}−\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{k}+\mathrm{n}\right)−\mathrm{ln}\left(\mathrm{n}\right)}{\mathrm{n}^{\mathrm{2}} \:+\mathrm{k}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{S}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{n}}\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}−\mathrm{1}} \:\frac{\mathrm{ln}\left(\frac{\mathrm{n}+\mathrm{k}}{\mathrm{n}}\right)}{\mathrm{1}+\frac{\mathrm{k}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }}\:=\frac{\mathrm{1}}{\mathrm{n}}\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}−\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)}{\mathrm{1}+\left(\frac{\mathrm{k}}{\mathrm{n}}\right)^{\mathrm{2}} }\:\mathrm{so}\:\mathrm{S}_{\mathrm{n}} \mathrm{is}\:\mathrm{a}\:\mathrm{Rieman}\:\mathrm{sum} \\ $$$$\mathrm{and}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{S}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{x}=\mathrm{tant}\:\mathrm{give} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{tant}\right)}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{t}}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{t}\right)\mathrm{dt}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{tan}\left(\mathrm{t}\right)\right)\mathrm{dt} \\ $$$$=_{\mathrm{t}=\frac{\pi}{\mathrm{4}}−\mathrm{u}} \:\:\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{1}+\mathrm{tan}\left(\frac{\pi}{\mathrm{4}}−\mathrm{u}\right)\right)\mathrm{du}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}−\mathrm{tanu}}{\mathrm{1}+\mathrm{tanu}}\right)\mathrm{du} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{ln}\left(\frac{\mathrm{2}}{\mathrm{1}+\mathrm{tanu}}\right)\mathrm{du}\:=\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right)−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{tanu}\right)\mathrm{du}\:\Rightarrow \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{tanu}\right)\mathrm{du}\:=\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right)\:\Rightarrow\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{1}+\mathrm{tanu}\right)\mathrm{du}\:=\frac{\pi}{\mathrm{8}}\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{S}_{\mathrm{n}} \\ $$

Commented by mathdave last updated on 08/Sep/20