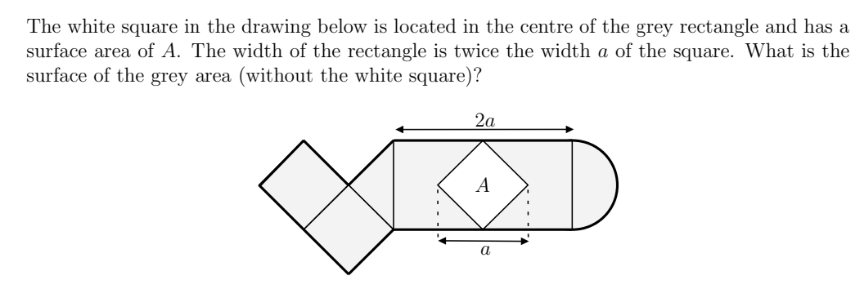
Question Number 112467 by Aina Samuel Temidayo last updated on 08/Sep/20
Answered by 1549442205PVT last updated on 08/Sep/20

$$\mathrm{Side}\:\mathrm{of}\:\mathrm{the}\:\mathrm{square}\:\mathrm{equal}\:\mathrm{to}\:\frac{\mathrm{a}}{\:\sqrt{\mathrm{2}}} \\ $$$$\mathrm{Width}\:\mathrm{of}\:\mathrm{rectangle}\:\mathrm{equal}\:\mathrm{to}\:\frac{\mathrm{2a}}{\:\sqrt{\mathrm{2}}}=\mathrm{a}\sqrt{\mathrm{2}} \\ $$$$\mathrm{The}\:\mathrm{area}\:\mathrm{of}\:\mathrm{rectangle}\:\mathrm{is}\:\mathrm{S}_{\mathrm{1}} =\mathrm{2a}.\mathrm{a}\sqrt{\mathrm{2}}=\mathrm{2a}^{\mathrm{2}} \sqrt{\mathrm{2}}\:\left(\mathrm{1}\right) \\ $$$$\mathrm{The}\:\mathrm{area}\:\mathrm{of}\:\mathrm{semicircle}\:\mathrm{equal}\:\mathrm{to}\:\frac{\mathrm{1}}{\mathrm{2}}\pi\left(\frac{\mathrm{a}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} \\ $$$$=\frac{\pi\mathrm{a}^{\mathrm{2}} }{\mathrm{16}}\left(\mathrm{2}\right).\mathrm{Side}\:\mathrm{of}\:\mathrm{the}\:\mathrm{right}\:\mathrm{triangle}\:\mathrm{equal}\:\mathrm{to} \\ $$$$\frac{\mathrm{a}\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}}=\mathrm{a}−\mathrm{this}\:\mathrm{is}\:\mathrm{also}\:\mathrm{side}\:\mathrm{of}\:\mathrm{two}\:\mathrm{squares} \\ $$$$\mathrm{The}\:\mathrm{area}\:\mathrm{of}\:\mathrm{two}\:\mathrm{squares}\:\mathrm{and} \\ $$$$\mathrm{triangle}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{2a}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\mathrm{a}^{\mathrm{2}} \\ $$$$=\frac{\mathrm{5}}{\mathrm{2}}.\mathrm{a}^{\mathrm{2}} =\left(\mathrm{3}\right) \\ $$$$\mathrm{From}\:\left(\mathrm{1}\right)\left(\mathrm{2}\right)\left(\mathrm{3}\right)\:\mathrm{we}\:\mathrm{infer}\:\mathrm{grey}\:\mathrm{area}\: \\ $$$$\mathrm{equal}\:\mathrm{to}\:\mathrm{2a}^{\mathrm{2}} \sqrt{\mathrm{2}}\:+\frac{\pi\mathrm{a}^{\mathrm{2}} }{\mathrm{16}}+\frac{\mathrm{5}}{\mathrm{2}}\mathrm{a}^{\mathrm{2}} −\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$=\frac{\boldsymbol{\mathrm{a}}^{\mathrm{2}} \left(\boldsymbol{\pi}+\mathrm{32}+\mathrm{32}\sqrt{\mathrm{2}}\right)}{\mathrm{16}} \\ $$
Commented by Aina Samuel Temidayo last updated on 08/Sep/20

$$\mathrm{Ok}.\:\mathrm{Thanks}. \\ $$
Commented by 1549442205PVT last updated on 13/Sep/20

$$\mathrm{You}\:\mathrm{are}\:\mathrm{welcome} \\ $$
Commented by Aina Samuel Temidayo last updated on 13/Sep/20

$$\mathrm{Is}\:\mathrm{your}\:\mathrm{User}\:\mathrm{ID}\:'…'\:? \\ $$
Commented by Rasheed.Sindhi last updated on 21/Sep/20
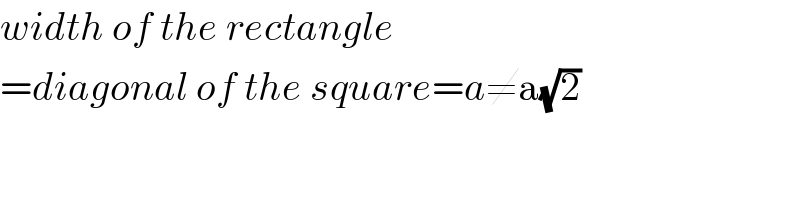
$${width}\:{of}\:{the}\:{rectangle} \\ $$$$={diagonal}\:{of}\:{the}\:{square}={a}\neq\mathrm{a}\sqrt{\mathrm{2}} \\ $$
Commented by 1549442205PVT last updated on 21/Sep/20
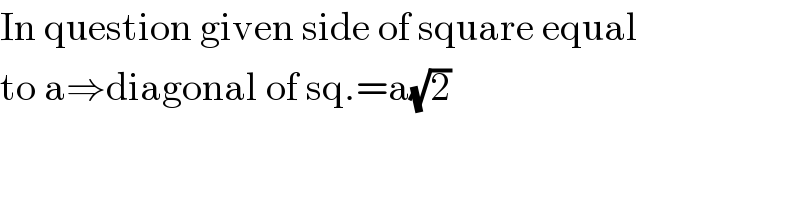
$$\mathrm{In}\:\mathrm{question}\:\mathrm{given}\:\mathrm{side}\:\mathrm{of}\:\mathrm{square}\:\mathrm{equal} \\ $$$$\mathrm{to}\:\mathrm{a}\Rightarrow\mathrm{diagonal}\:\mathrm{of}\:\mathrm{sq}.=\mathrm{a}\sqrt{\mathrm{2}} \\ $$
Commented by Rasheed.Sindhi last updated on 21/Sep/20
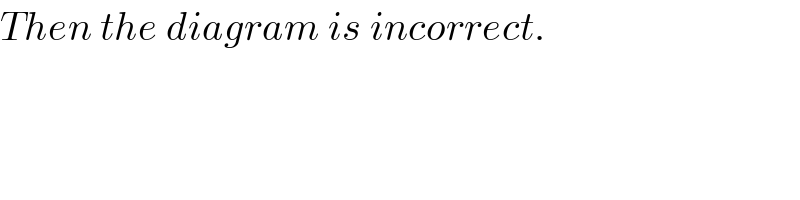
$${Then}\:{the}\:{diagram}\:{is}\:{incorrect}. \\ $$
