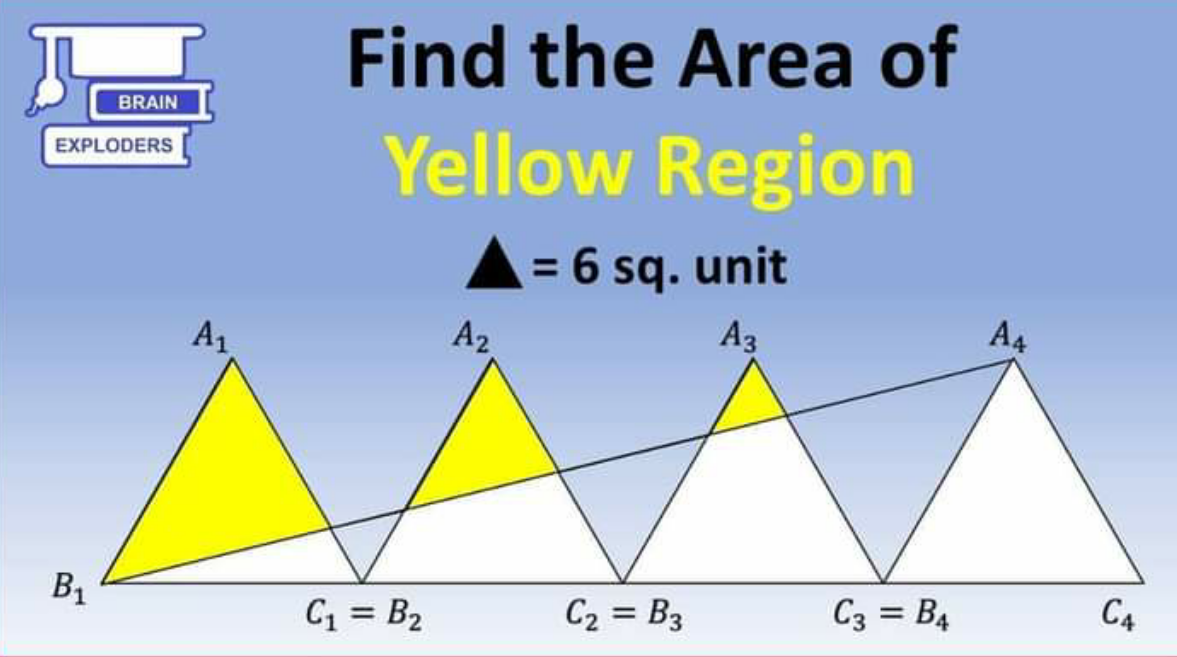
Question Number 112500 by I want to learn more last updated on 08/Sep/20
Answered by 1549442205PVT last updated on 08/Sep/20
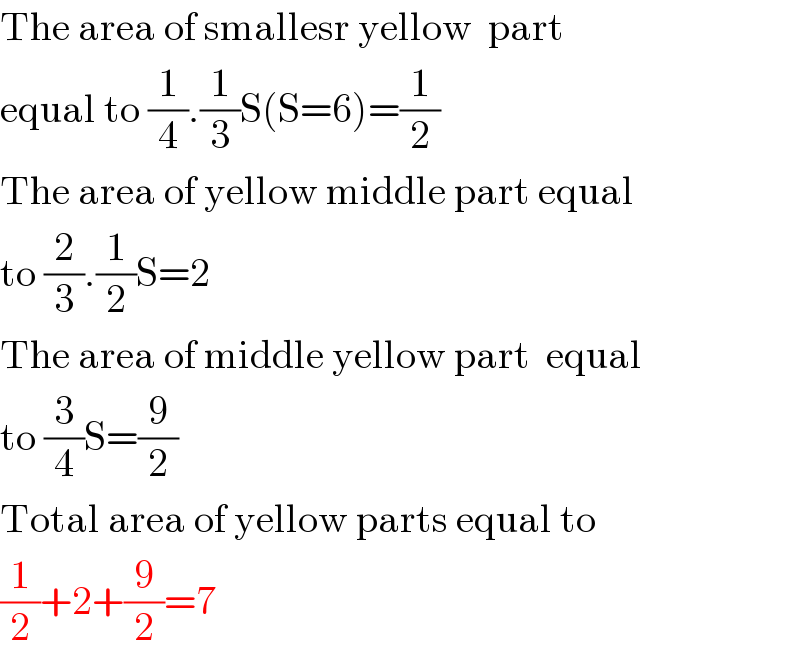
$$\mathrm{The}\:\mathrm{area}\:\mathrm{of}\:\mathrm{smallesr}\:\mathrm{yellow}\:\:\mathrm{part} \\ $$$$\mathrm{equal}\:\mathrm{to}\:\frac{\mathrm{1}}{\mathrm{4}}.\frac{\mathrm{1}}{\mathrm{3}}\mathrm{S}\left(\mathrm{S}=\mathrm{6}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{The}\:\mathrm{area}\:\mathrm{of}\:\mathrm{yellow}\:\mathrm{middle}\:\mathrm{part}\:\mathrm{equal} \\ $$$$\mathrm{to}\:\frac{\mathrm{2}}{\mathrm{3}}.\frac{\mathrm{1}}{\mathrm{2}}\mathrm{S}=\mathrm{2} \\ $$$$\mathrm{The}\:\mathrm{area}\:\mathrm{of}\:\mathrm{middle}\:\mathrm{yellow}\:\mathrm{part}\:\:\mathrm{equal}\: \\ $$$$\mathrm{to}\:\frac{\mathrm{3}}{\mathrm{4}}\mathrm{S}=\frac{\mathrm{9}}{\mathrm{2}} \\ $$$$\mathrm{Total}\:\mathrm{area}\:\mathrm{of}\:\mathrm{yellow}\:\mathrm{parts}\:\mathrm{equal}\:\mathrm{to} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{2}+\frac{\mathrm{9}}{\mathrm{2}}=\mathrm{7} \\ $$
Commented by I want to learn more last updated on 08/Sep/20

$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate} \\ $$
Commented by 1549442205PVT last updated on 13/Sep/20

$$\mathrm{You}\:\mathrm{are}\:\mathrm{welcome} \\ $$
