Question Number 112502 by bemath last updated on 08/Sep/20

Answered by floor(10²Eta[1]) last updated on 08/Sep/20
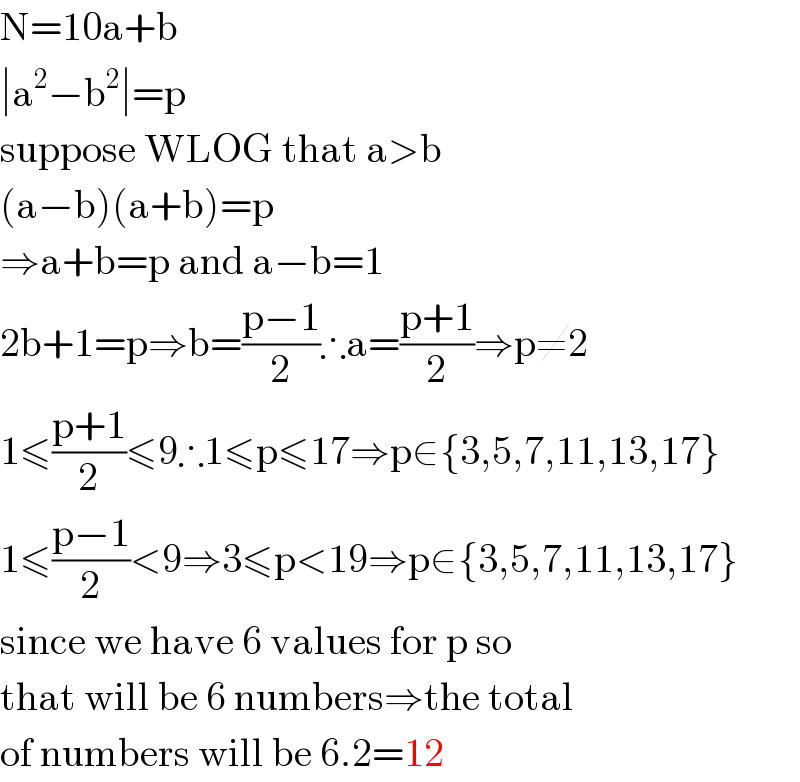
$$\mathrm{N}=\mathrm{10a}+\mathrm{b} \\ $$$$\mid\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \mid=\mathrm{p} \\ $$$$\mathrm{suppose}\:\mathrm{WLOG}\:\mathrm{that}\:\mathrm{a}>\mathrm{b} \\ $$$$\left(\mathrm{a}−\mathrm{b}\right)\left(\mathrm{a}+\mathrm{b}\right)=\mathrm{p} \\ $$$$\Rightarrow\mathrm{a}+\mathrm{b}=\mathrm{p}\:\mathrm{and}\:\mathrm{a}−\mathrm{b}=\mathrm{1} \\ $$$$\mathrm{2b}+\mathrm{1}=\mathrm{p}\Rightarrow\mathrm{b}=\frac{\mathrm{p}−\mathrm{1}}{\mathrm{2}}\therefore\mathrm{a}=\frac{\mathrm{p}+\mathrm{1}}{\mathrm{2}}\Rightarrow\mathrm{p}\neq\mathrm{2} \\ $$$$\mathrm{1}\leqslant\frac{\mathrm{p}+\mathrm{1}}{\mathrm{2}}\leqslant\mathrm{9}\therefore\mathrm{1}\leqslant\mathrm{p}\leqslant\mathrm{17}\Rightarrow\mathrm{p}\in\left\{\mathrm{3},\mathrm{5},\mathrm{7},\mathrm{11},\mathrm{13},\mathrm{17}\right\} \\ $$$$\mathrm{1}\leqslant\frac{\mathrm{p}−\mathrm{1}}{\mathrm{2}}<\mathrm{9}\Rightarrow\mathrm{3}\leqslant\mathrm{p}<\mathrm{19}\Rightarrow\mathrm{p}\in\left\{\mathrm{3},\mathrm{5},\mathrm{7},\mathrm{11},\mathrm{13},\mathrm{17}\right\} \\ $$$$\mathrm{since}\:\mathrm{we}\:\mathrm{have}\:\mathrm{6}\:\mathrm{values}\:\mathrm{for}\:\mathrm{p}\:\mathrm{so} \\ $$$$\mathrm{that}\:\mathrm{will}\:\mathrm{be}\:\mathrm{6}\:\mathrm{numbers}\Rightarrow\mathrm{the}\:\mathrm{total} \\ $$$$\mathrm{of}\:\mathrm{numbers}\:\mathrm{will}\:\mathrm{be}\:\mathrm{6}.\mathrm{2}=\mathrm{12} \\ $$
