Question Number 112538 by Aina Samuel Temidayo last updated on 08/Sep/20

Answered by floor(10²Eta[1]) last updated on 08/Sep/20
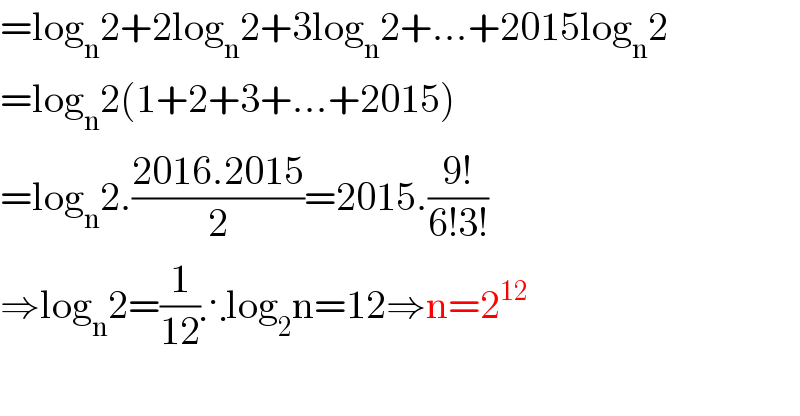
$$=\mathrm{log}_{\mathrm{n}} \mathrm{2}+\mathrm{2log}_{\mathrm{n}} \mathrm{2}+\mathrm{3log}_{\mathrm{n}} \mathrm{2}+…+\mathrm{2015log}_{\mathrm{n}} \mathrm{2} \\ $$$$=\mathrm{log}_{\mathrm{n}} \mathrm{2}\left(\mathrm{1}+\mathrm{2}+\mathrm{3}+…+\mathrm{2015}\right) \\ $$$$=\mathrm{log}_{\mathrm{n}} \mathrm{2}.\frac{\mathrm{2016}.\mathrm{2015}}{\mathrm{2}}=\mathrm{2015}.\frac{\mathrm{9}!}{\mathrm{6}!\mathrm{3}!} \\ $$$$\Rightarrow\mathrm{log}_{\mathrm{n}} \mathrm{2}=\frac{\mathrm{1}}{\mathrm{12}}\therefore\mathrm{log}_{\mathrm{2}} \mathrm{n}=\mathrm{12}\Rightarrow\mathrm{n}=\mathrm{2}^{\mathrm{12}} \\ $$$$ \\ $$
Commented by Aina Samuel Temidayo last updated on 08/Sep/20

$$\mathrm{Thanks}. \\ $$
