Question Number 112575 by Aina Samuel Temidayo last updated on 08/Sep/20
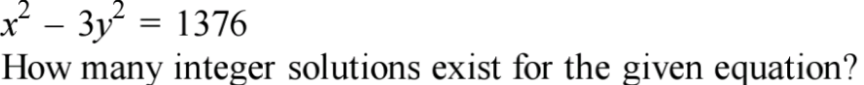
Answered by Rasheed.Sindhi last updated on 09/Sep/20
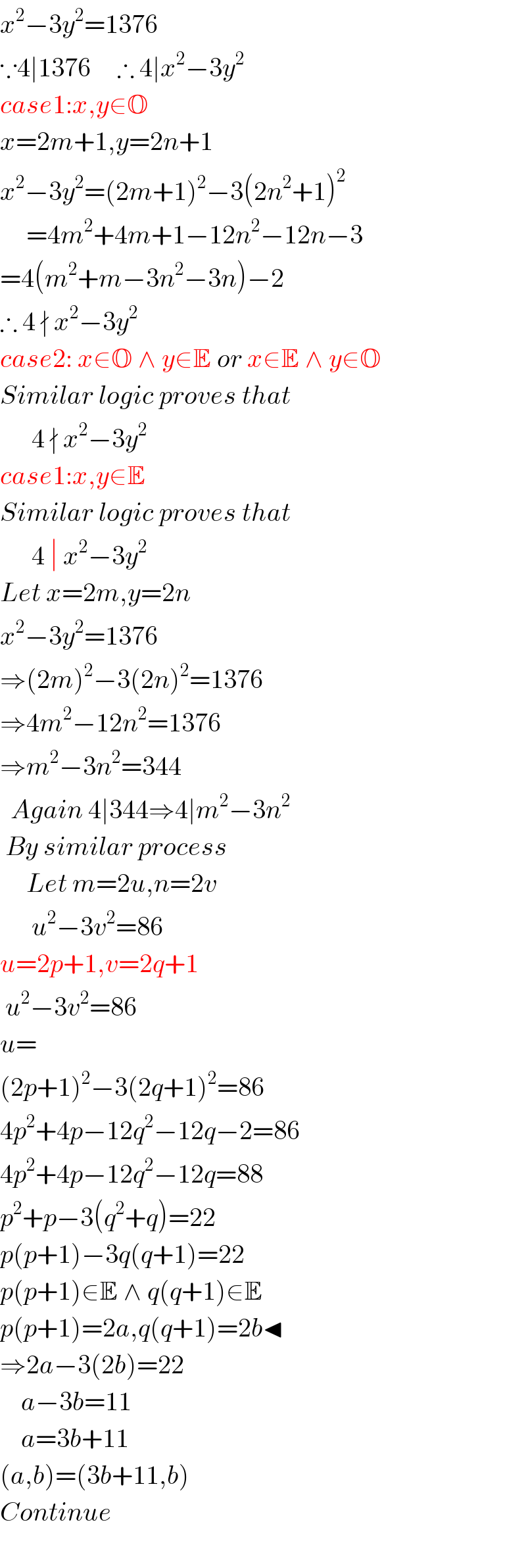
$${x}^{\mathrm{2}} −\mathrm{3}{y}^{\mathrm{2}} =\mathrm{1376} \\ $$$$\because\mathrm{4}\mid\mathrm{1376}\:\:\:\:\:\therefore\:\mathrm{4}\mid{x}^{\mathrm{2}} −\mathrm{3}{y}^{\mathrm{2}} \\ $$$${case}\mathrm{1}:{x},{y}\in\mathbb{O} \\ $$$${x}=\mathrm{2}{m}+\mathrm{1},{y}=\mathrm{2}{n}+\mathrm{1} \\ $$$${x}^{\mathrm{2}} −\mathrm{3}{y}^{\mathrm{2}} =\left(\mathrm{2}{m}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{3}\left(\mathrm{2}{n}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:=\mathrm{4}{m}^{\mathrm{2}} +\mathrm{4}{m}+\mathrm{1}−\mathrm{12}{n}^{\mathrm{2}} −\mathrm{12}{n}−\mathrm{3} \\ $$$$=\mathrm{4}\left({m}^{\mathrm{2}} +{m}−\mathrm{3}{n}^{\mathrm{2}} −\mathrm{3}{n}\right)−\mathrm{2} \\ $$$$\therefore\:\mathrm{4}\:\nmid\:{x}^{\mathrm{2}} −\mathrm{3}{y}^{\mathrm{2}} \\ $$$${case}\mathrm{2}:\:{x}\in\mathbb{O}\:\wedge\:{y}\in\mathbb{E}\:{or}\:{x}\in\mathbb{E}\:\wedge\:{y}\in\mathbb{O} \\ $$$${Similar}\:{logic}\:{proves}\:{that} \\ $$$$\:\:\:\:\:\:\mathrm{4}\:\nmid\:{x}^{\mathrm{2}} −\mathrm{3}{y}^{\mathrm{2}} \\ $$$${case}\mathrm{1}:{x},{y}\in\mathbb{E} \\ $$$${Similar}\:{logic}\:{proves}\:{that} \\ $$$$\:\:\:\:\:\:\mathrm{4}\:\mid\:{x}^{\mathrm{2}} −\mathrm{3}{y}^{\mathrm{2}} \\ $$$${Let}\:{x}=\mathrm{2}{m},{y}=\mathrm{2}{n} \\ $$$${x}^{\mathrm{2}} −\mathrm{3}{y}^{\mathrm{2}} =\mathrm{1376} \\ $$$$\Rightarrow\left(\mathrm{2}{m}\right)^{\mathrm{2}} −\mathrm{3}\left(\mathrm{2}{n}\right)^{\mathrm{2}} =\mathrm{1376} \\ $$$$\Rightarrow\mathrm{4}{m}^{\mathrm{2}} −\mathrm{12}{n}^{\mathrm{2}} =\mathrm{1376} \\ $$$$\Rightarrow{m}^{\mathrm{2}} −\mathrm{3}{n}^{\mathrm{2}} =\mathrm{344} \\ $$$$\:\:{Again}\:\mathrm{4}\mid\mathrm{344}\Rightarrow\mathrm{4}\mid{m}^{\mathrm{2}} −\mathrm{3}{n}^{\mathrm{2}} \\ $$$$\:{By}\:{similar}\:{process} \\ $$$$\:\:\:\:\:{Let}\:{m}=\mathrm{2}{u},{n}=\mathrm{2}{v} \\ $$$$\:\:\:\:\:\:{u}^{\mathrm{2}} −\mathrm{3}{v}^{\mathrm{2}} =\mathrm{86} \\ $$$${u}=\mathrm{2}{p}+\mathrm{1},{v}=\mathrm{2}{q}+\mathrm{1} \\ $$$$\:{u}^{\mathrm{2}} −\mathrm{3}{v}^{\mathrm{2}} =\mathrm{86} \\ $$$${u}= \\ $$$$\left(\mathrm{2}{p}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{3}\left(\mathrm{2}{q}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{86} \\ $$$$\mathrm{4}{p}^{\mathrm{2}} +\mathrm{4}{p}−\mathrm{12}{q}^{\mathrm{2}} −\mathrm{12}{q}−\mathrm{2}=\mathrm{86} \\ $$$$\mathrm{4}{p}^{\mathrm{2}} +\mathrm{4}{p}−\mathrm{12}{q}^{\mathrm{2}} −\mathrm{12}{q}=\mathrm{88} \\ $$$${p}^{\mathrm{2}} +{p}−\mathrm{3}\left({q}^{\mathrm{2}} +{q}\right)=\mathrm{22} \\ $$$${p}\left({p}+\mathrm{1}\right)−\mathrm{3}{q}\left({q}+\mathrm{1}\right)=\mathrm{22} \\ $$$${p}\left({p}+\mathrm{1}\right)\in\mathbb{E}\:\wedge\:{q}\left({q}+\mathrm{1}\right)\in\mathbb{E} \\ $$$${p}\left({p}+\mathrm{1}\right)=\mathrm{2}{a},{q}\left({q}+\mathrm{1}\right)=\mathrm{2}{b}\blacktriangleleft \\ $$$$\Rightarrow\mathrm{2}{a}−\mathrm{3}\left(\mathrm{2}{b}\right)=\mathrm{22} \\ $$$$\:\:\:\:{a}−\mathrm{3}{b}=\mathrm{11} \\ $$$$\:\:\:\:{a}=\mathrm{3}{b}+\mathrm{11} \\ $$$$\left({a},{b}\right)=\left(\mathrm{3}{b}+\mathrm{11},{b}\right) \\ $$$${Continue} \\ $$$$ \\ $$
Commented by Aina Samuel Temidayo last updated on 09/Sep/20
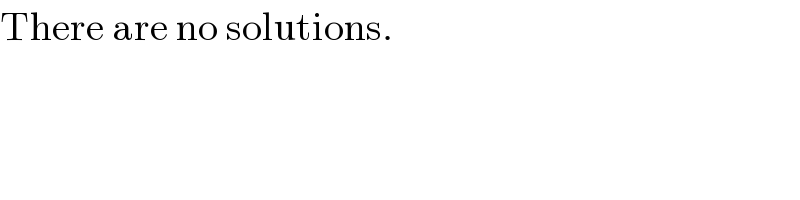
$$\mathrm{There}\:\mathrm{are}\:\mathrm{no}\:\mathrm{solutions}. \\ $$
