Menu Close

Question-112576

Tinku Tara 0 Comments
Pin




Question Number 112576 by ajfour last updated on 08/Sep/20
Commented by ajfour last updated on 08/Sep/20
Find OA=AB.
$${Find}\:{OA}={AB}. \\ $$
Answered by mr W last updated on 09/Sep/20
A(a,a^2 ) B(−b,b^2 ) eqn. of OA: y=ax eqn. of AB: y=a^2 −(1/a)(x−a)=a^2 +1−(x/a) b^2 =a^2 +1+(b/a) a^2 −b^2 a+b+1=0 ⇒a=((b^2 ±(√(b^4 −4(b+1))))/2) (b^2 −a^2 )^2 +(a+b)^2 =a^4 +a^2 2ba^2 −2a−b(1+b^2 )=0 ⇒a=((1+(√(1+2b^2 (1+b^2 ))))/(2b)) ...
$${A}\left({a},{a}^{\mathrm{2}} \right) \\ $$$${B}\left(−{b},{b}^{\mathrm{2}} \right) \\ $$$${eqn}.\:{of}\:{OA}: \\ $$$${y}={ax} \\ $$$${eqn}.\:{of}\:{AB}: \\ $$$${y}={a}^{\mathrm{2}} −\frac{\mathrm{1}}{{a}}\left({x}−{a}\right)={a}^{\mathrm{2}} +\mathrm{1}−\frac{{x}}{{a}} \\ $$$${b}^{\mathrm{2}} ={a}^{\mathrm{2}} +\mathrm{1}+\frac{{b}}{{a}} \\ $$$${a}^{\mathrm{2}} −{b}^{\mathrm{2}} {a}+{b}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{a}=\frac{{b}^{\mathrm{2}} \pm\sqrt{{b}^{\mathrm{4}} −\mathrm{4}\left({b}+\mathrm{1}\right)}}{\mathrm{2}} \\ $$$$\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)^{\mathrm{2}} +\left({a}+{b}\right)^{\mathrm{2}} ={a}^{\mathrm{4}} +{a}^{\mathrm{2}} \\ $$$$\mathrm{2}{ba}^{\mathrm{2}} −\mathrm{2}{a}−{b}\left(\mathrm{1}+{b}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow{a}=\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{2}{b}^{\mathrm{2}} \left(\mathrm{1}+{b}^{\mathrm{2}} \right)}}{\mathrm{2}{b}} \\ $$$$… \\ $$
Commented by mr W last updated on 09/Sep/20
you are right. thanks sir!
$${you}\:{are}\:{right}.\:{thanks}\:{sir}! \\ $$
Answered by ajfour last updated on 08/Sep/20
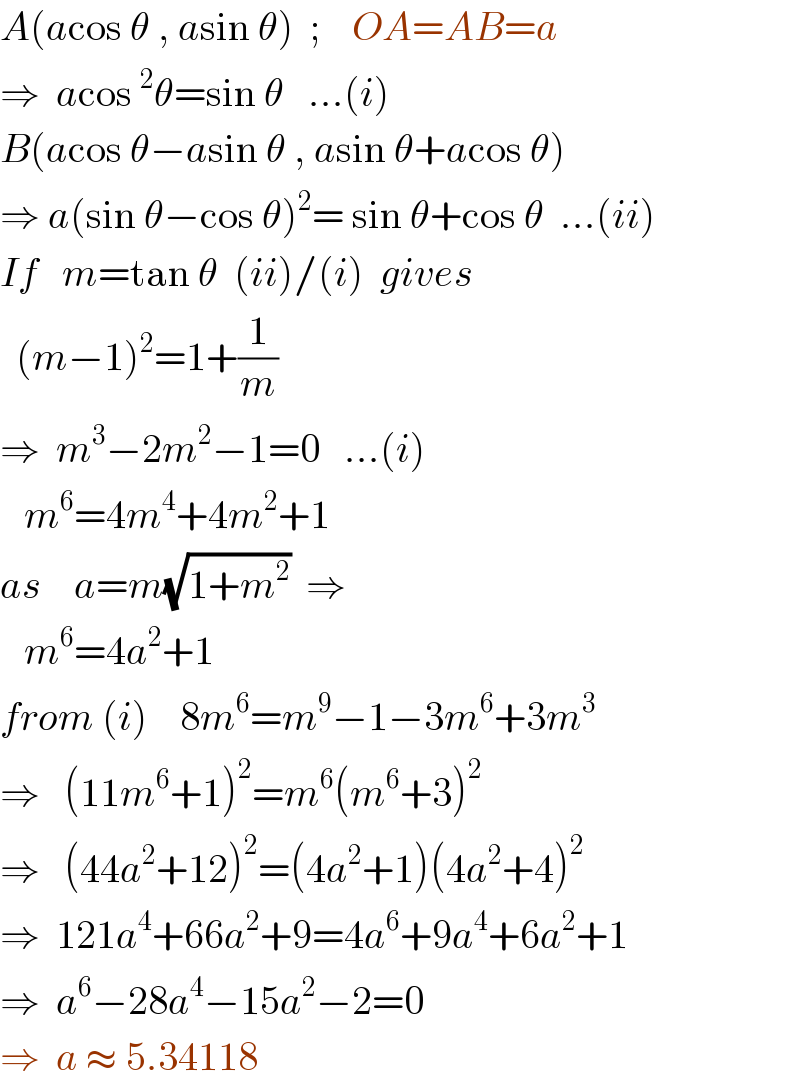
A(acos θ , asin θ) ; OA=AB=a ⇒ acos^2 θ=sin θ ...(i) B(acos θ−asin θ , asin θ+acos θ) ⇒ a(sin θ−cos θ)^2 = sin θ+cos θ ...(ii) If m=tan θ (ii)/(i) gives (m−1)^2 =1+(1/m) ⇒ m^3 −2m^2 −1=0 ...(i) m^6 =4m^4 +4m^2 +1 as a=m(√(1+m^2 )) ⇒ m^6 =4a^2 +1 from (i) 8m^6 =m^9 −1−3m^6 +3m^3 ⇒ (11m^6 +1)^2 =m^6 (m^6 +3)^2 ⇒ (44a^2 +12)^2 =(4a^2 +1)(4a^2 +4)^2 ⇒ 121a^4 +66a^2 +9=4a^6 +9a^4 +6a^2 +1 ⇒ a^6 −28a^4 −15a^2 −2=0 ⇒ a ≈ 5.34118
$${A}\left({a}\mathrm{cos}\:\theta\:,\:{a}\mathrm{sin}\:\theta\right)\:\:;\:\:\:\:{OA}={AB}={a} \\ $$$$\Rightarrow\:\:{a}\mathrm{cos}\:^{\mathrm{2}} \theta=\mathrm{sin}\:\theta\:\:\:…\left({i}\right) \\ $$$${B}\left({a}\mathrm{cos}\:\theta−{a}\mathrm{sin}\:\theta\:,\:{a}\mathrm{sin}\:\theta+{a}\mathrm{cos}\:\theta\right) \\ $$$$\Rightarrow\:{a}\left(\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\right)^{\mathrm{2}} =\:\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\:\:…\left({ii}\right) \\ $$$${If}\:\:\:{m}=\mathrm{tan}\:\theta\:\:\left({ii}\right)/\left({i}\right)\:\:{gives} \\ $$$$\:\:\left({m}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{1}+\frac{\mathrm{1}}{{m}} \\ $$$$\Rightarrow\:\:{m}^{\mathrm{3}} −\mathrm{2}{m}^{\mathrm{2}} −\mathrm{1}=\mathrm{0}\:\:\:…\left({i}\right) \\ $$$$\:\:\:{m}^{\mathrm{6}} =\mathrm{4}{m}^{\mathrm{4}} +\mathrm{4}{m}^{\mathrm{2}} +\mathrm{1} \\ $$$${as}\:\:\:\:{a}={m}\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }\:\:\Rightarrow \\ $$$$\:\:\:{m}^{\mathrm{6}} =\mathrm{4}{a}^{\mathrm{2}} +\mathrm{1} \\ $$$${from}\:\left({i}\right)\:\:\:\:\mathrm{8}{m}^{\mathrm{6}} ={m}^{\mathrm{9}} −\mathrm{1}−\mathrm{3}{m}^{\mathrm{6}} +\mathrm{3}{m}^{\mathrm{3}} \\ $$$$\Rightarrow\:\:\:\left(\mathrm{11}{m}^{\mathrm{6}} +\mathrm{1}\right)^{\mathrm{2}} ={m}^{\mathrm{6}} \left({m}^{\mathrm{6}} +\mathrm{3}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\left(\mathrm{44}{a}^{\mathrm{2}} +\mathrm{12}\right)^{\mathrm{2}} =\left(\mathrm{4}{a}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{4}{a}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{121}{a}^{\mathrm{4}} +\mathrm{66}{a}^{\mathrm{2}} +\mathrm{9}=\mathrm{4}{a}^{\mathrm{6}} +\mathrm{9}{a}^{\mathrm{4}} +\mathrm{6}{a}^{\mathrm{2}} +\mathrm{1} \\ $$$$\Rightarrow\:\:{a}^{\mathrm{6}} −\mathrm{28}{a}^{\mathrm{4}} −\mathrm{15}{a}^{\mathrm{2}} −\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\:\:{a}\:\approx\:\mathrm{5}.\mathrm{34118} \\ $$
Commented by ajfour last updated on 08/Sep/20
Commented by mr W last updated on 09/Sep/20
nice solution!
$${nice}\:{solution}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *