Question Number 112606 by ajfour last updated on 08/Sep/20
Commented by ajfour last updated on 10/Sep/20

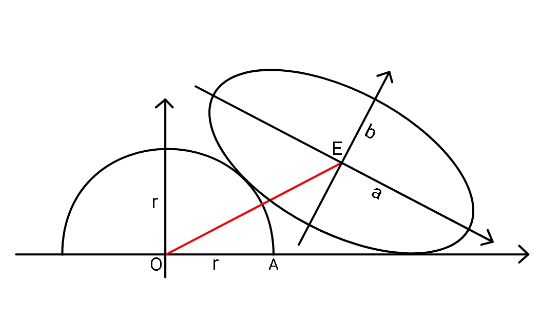
$${Find}\:{minimum}\:{length}\:{of}\:{AE}\:{in} \\ $$$${terms}\:{of}\:{r},\:{a},\:{b}.\:\:\: \\ $$
Answered by mr W last updated on 09/Sep/20
Commented by mr W last updated on 09/Sep/20
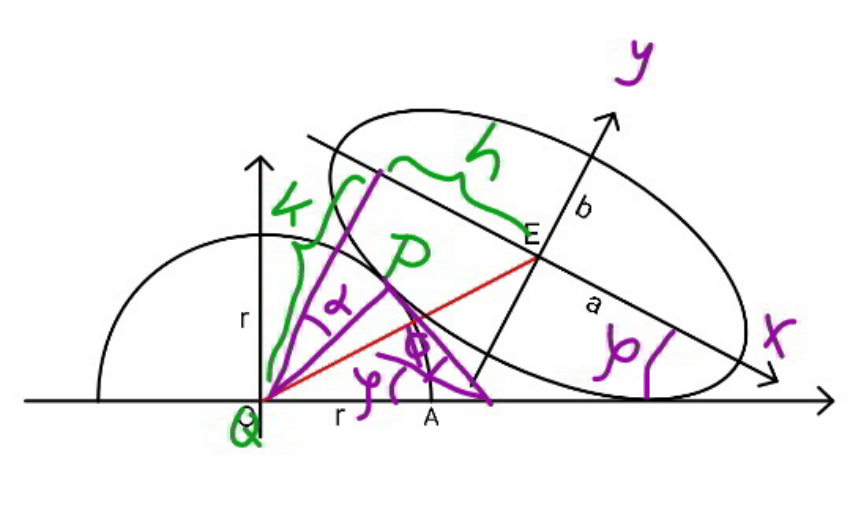
![μ=(b/a) ρ=(r/a) η=(h/a) λ=tan ϕ eqn. of QA: y=−k+(x+h)tan ϕ λx−y+(λh−k)=0 λ^2 a^2 +b^2 =(λh−k)^2 ⇒k=λh−(√(λ^2 a^2 +b^2 )) ⇒(k/a)=λη−(√(λ^2 +μ^2 )) P(−a cos θ, −b sin θ) tan φ=(μ/(tan θ)) ϕ+α+((π/2)−ϕ−φ)=(π/2) ⇒α⇒φ −a cos θ=−h+r sin φ ⇒ρ sin φ=η−cos θ −b sin θ=−k+r cos φ ⇒ρ cos φ=λη−(√(λ^2 +μ^2 ))−μ sin θ ⇒tan φ=((η−cos θ)/(λη−(√(λ^2 +μ^2 ))−μ sin θ)) ⇒(μ/(tan θ))=((η−cos θ)/(λη−(√(λ^2 +μ^2 ))−μ sin θ)) (μλ−tan θ)η=μ(√(λ^2 +μ^2 ))−(1−μ^2 )sin θ ⇒η=((μ(√(λ^2 +μ^2 ))−(1−μ^2 )sin θ)/(μλ−tan θ)) ⇒ρ^2 =(η−cos θ)^2 +(λη−(√(λ^2 +μ^2 ))−μ sin θ)^2 x_A =−h+r cos ϕ y_A =−k+r sin ϕ AE^2 =(h−r cos ϕ)^2 +(k−r sin ϕ)^2 Φ=(((AE)/a))^2 =(η−ρ cos ϕ)^2 +(λη−(√(λ^2 +μ^2 ))−ρ sin ϕ)^2 Φ=[((μ(√(λ^2 +μ^2 ))−(1−μ^2 )sin θ)/(μλ−tan θ))−ρ cos ϕ]^2 +[((μλ(√(λ^2 +μ^2 ))−λ(1−μ^2 )sin θ)/(μλ−tan θ))−(√(λ^2 +μ^2 ))−ρ sin ϕ]^2 .....](https://www.tinkutara.com/question/Q112826.png)
$$\mu=\frac{{b}}{{a}} \\ $$$$\rho=\frac{{r}}{{a}} \\ $$$$\eta=\frac{{h}}{{a}} \\ $$$$\lambda=\mathrm{tan}\:\varphi \\ $$$${eqn}.\:{of}\:{QA}: \\ $$$${y}=−{k}+\left({x}+{h}\right)\mathrm{tan}\:\varphi \\ $$$$\lambda{x}−{y}+\left(\lambda{h}−{k}\right)=\mathrm{0} \\ $$$$\lambda^{\mathrm{2}} {a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\left(\lambda{h}−{k}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{k}=\lambda{h}−\sqrt{\lambda^{\mathrm{2}} {a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{{k}}{{a}}=\lambda\eta−\sqrt{\lambda^{\mathrm{2}} +\mu^{\mathrm{2}} } \\ $$$${P}\left(−{a}\:\mathrm{cos}\:\theta,\:−{b}\:\mathrm{sin}\:\theta\right) \\ $$$$\mathrm{tan}\:\phi=\frac{\mu}{\mathrm{tan}\:\theta} \\ $$$$\varphi+\alpha+\left(\frac{\pi}{\mathrm{2}}−\varphi−\phi\right)=\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\alpha\Rightarrow\phi \\ $$$$−{a}\:\mathrm{cos}\:\theta=−{h}+{r}\:\mathrm{sin}\:\phi \\ $$$$\Rightarrow\rho\:\mathrm{sin}\:\phi=\eta−\mathrm{cos}\:\theta \\ $$$$−{b}\:\mathrm{sin}\:\theta=−{k}+{r}\:\mathrm{cos}\:\phi \\ $$$$\Rightarrow\rho\:\mathrm{cos}\:\phi=\lambda\eta−\sqrt{\lambda^{\mathrm{2}} +\mu^{\mathrm{2}} }−\mu\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow\mathrm{tan}\:\phi=\frac{\eta−\mathrm{cos}\:\theta}{\lambda\eta−\sqrt{\lambda^{\mathrm{2}} +\mu^{\mathrm{2}} }−\mu\:\mathrm{sin}\:\theta} \\ $$$$\Rightarrow\frac{\mu}{\mathrm{tan}\:\theta}=\frac{\eta−\mathrm{cos}\:\theta}{\lambda\eta−\sqrt{\lambda^{\mathrm{2}} +\mu^{\mathrm{2}} }−\mu\:\mathrm{sin}\:\theta} \\ $$$$\left(\mu\lambda−\mathrm{tan}\:\theta\right)\eta=\mu\sqrt{\lambda^{\mathrm{2}} +\mu^{\mathrm{2}} }−\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\mathrm{sin}\:\theta \\ $$$$\Rightarrow\eta=\frac{\mu\sqrt{\lambda^{\mathrm{2}} +\mu^{\mathrm{2}} }−\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\mathrm{sin}\:\theta}{\mu\lambda−\mathrm{tan}\:\theta} \\ $$$$\Rightarrow\rho^{\mathrm{2}} =\left(\eta−\mathrm{cos}\:\theta\right)^{\mathrm{2}} +\left(\lambda\eta−\sqrt{\lambda^{\mathrm{2}} +\mu^{\mathrm{2}} }−\mu\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} \\ $$$$ \\ $$$${x}_{{A}} =−{h}+{r}\:\mathrm{cos}\:\varphi \\ $$$${y}_{{A}} =−{k}+{r}\:\mathrm{sin}\:\varphi \\ $$$${AE}^{\mathrm{2}} =\left({h}−{r}\:\mathrm{cos}\:\varphi\right)^{\mathrm{2}} +\left({k}−{r}\:\mathrm{sin}\:\varphi\right)^{\mathrm{2}} \\ $$$$\Phi=\left(\frac{{AE}}{{a}}\right)^{\mathrm{2}} =\left(\eta−\rho\:\mathrm{cos}\:\varphi\right)^{\mathrm{2}} +\left(\lambda\eta−\sqrt{\lambda^{\mathrm{2}} +\mu^{\mathrm{2}} }−\rho\:\mathrm{sin}\:\varphi\right)^{\mathrm{2}} \\ $$$$\Phi=\left[\frac{\mu\sqrt{\lambda^{\mathrm{2}} +\mu^{\mathrm{2}} }−\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\mathrm{sin}\:\theta}{\mu\lambda−\mathrm{tan}\:\theta}−\rho\:\mathrm{cos}\:\varphi\right]^{\mathrm{2}} +\left[\frac{\mu\lambda\sqrt{\lambda^{\mathrm{2}} +\mu^{\mathrm{2}} }−\lambda\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\mathrm{sin}\:\theta}{\mu\lambda−\mathrm{tan}\:\theta}−\sqrt{\lambda^{\mathrm{2}} +\mu^{\mathrm{2}} }−\rho\:\mathrm{sin}\:\varphi\right]^{\mathrm{2}} \\ $$$$….. \\ $$
