Menu Close

Question-112751

Tinku Tara 0 Comments
Pin




Question Number 112751 by bemath last updated on 09/Sep/20
Answered by bobhans last updated on 09/Sep/20
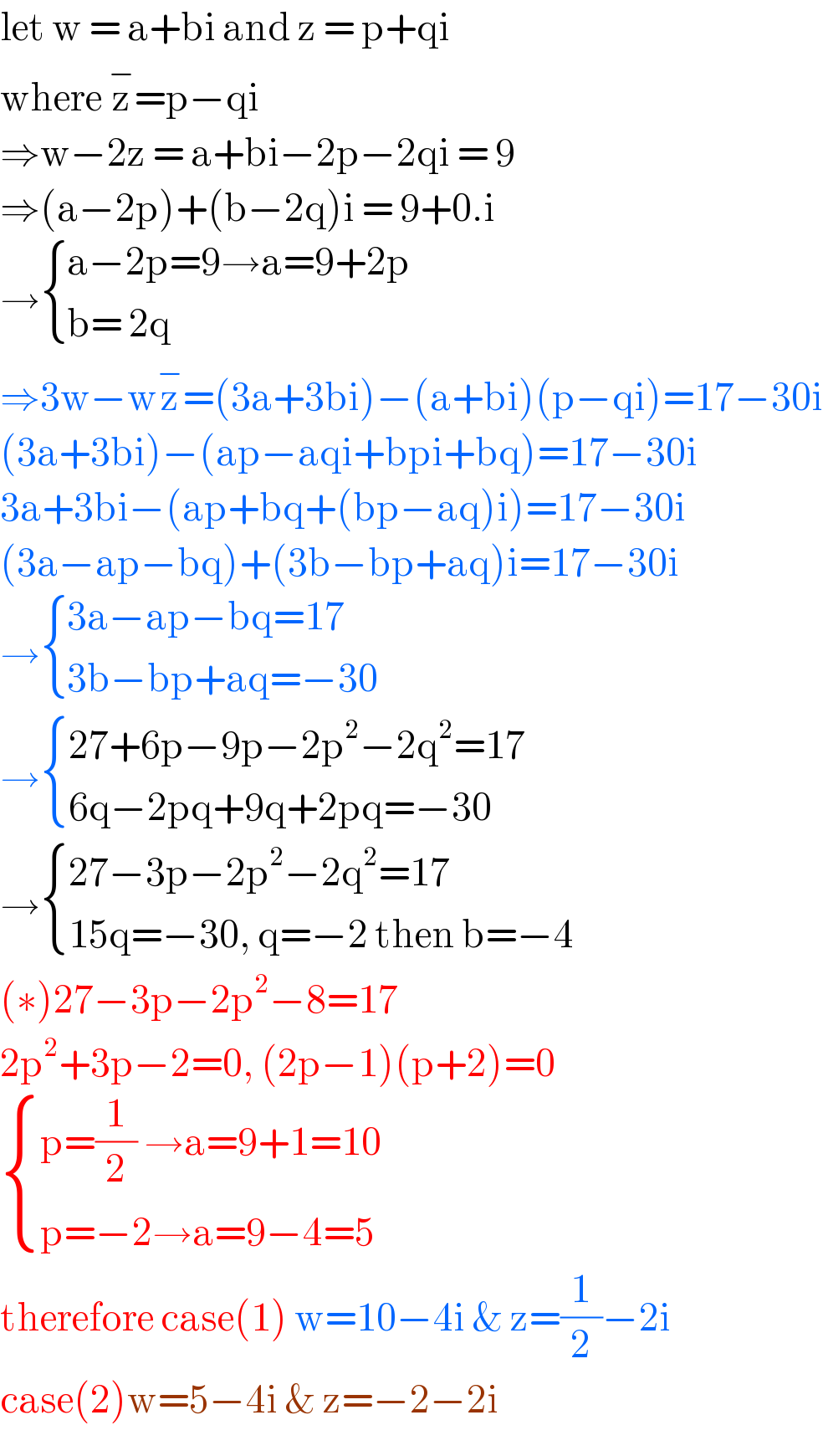
let w = a+bi and z = p+qi where z^− =p−qi ⇒w−2z = a+bi−2p−2qi = 9 ⇒(a−2p)+(b−2q)i = 9+0.i → { ((a−2p=9→a=9+2p)),((b= 2q)) :} ⇒3w−wz^− =(3a+3bi)−(a+bi)(p−qi)=17−30i (3a+3bi)−(ap−aqi+bpi+bq)=17−30i 3a+3bi−(ap+bq+(bp−aq)i)=17−30i (3a−ap−bq)+(3b−bp+aq)i=17−30i → { ((3a−ap−bq=17)),((3b−bp+aq=−30)) :} → { ((27+6p−9p−2p^2 −2q^2 =17)),((6q−2pq+9q+2pq=−30)) :} → { ((27−3p−2p^2 −2q^2 =17)),((15q=−30, q=−2 then b=−4)) :} (∗)27−3p−2p^2 −8=17 2p^2 +3p−2=0, (2p−1)(p+2)=0 { ((p=(1/2) →a=9+1=10)),((p=−2→a=9−4=5)) :} therefore case(1) w=10−4i & z=(1/2)−2i case(2)w=5−4i & z=−2−2i
$$\mathrm{let}\:\mathrm{w}\:=\:\mathrm{a}+\mathrm{bi}\:\mathrm{and}\:\mathrm{z}\:=\:\mathrm{p}+\mathrm{qi}\: \\ $$$$\mathrm{where}\:\overset{−} {\mathrm{z}}=\mathrm{p}−\mathrm{qi}\: \\ $$$$\Rightarrow\mathrm{w}−\mathrm{2z}\:=\:\mathrm{a}+\mathrm{bi}−\mathrm{2p}−\mathrm{2qi}\:=\:\mathrm{9} \\ $$$$\Rightarrow\left(\mathrm{a}−\mathrm{2p}\right)+\left(\mathrm{b}−\mathrm{2q}\right)\mathrm{i}\:=\:\mathrm{9}+\mathrm{0}.\mathrm{i} \\ $$$$\rightarrow\begin{cases}{\mathrm{a}−\mathrm{2p}=\mathrm{9}\rightarrow\mathrm{a}=\mathrm{9}+\mathrm{2p}}\\{\mathrm{b}=\:\mathrm{2q}}\end{cases} \\ $$$$\Rightarrow\mathrm{3w}−\mathrm{w}\overset{−} {\mathrm{z}}=\left(\mathrm{3a}+\mathrm{3bi}\right)−\left(\mathrm{a}+\mathrm{bi}\right)\left(\mathrm{p}−\mathrm{qi}\right)=\mathrm{17}−\mathrm{30i} \\ $$$$\left(\mathrm{3a}+\mathrm{3bi}\right)−\left(\mathrm{ap}−\mathrm{aqi}+\mathrm{bpi}+\mathrm{bq}\right)=\mathrm{17}−\mathrm{30i} \\ $$$$\mathrm{3a}+\mathrm{3bi}−\left(\mathrm{ap}+\mathrm{bq}+\left(\mathrm{bp}−\mathrm{aq}\right)\mathrm{i}\right)=\mathrm{17}−\mathrm{30i} \\ $$$$\left(\mathrm{3a}−\mathrm{ap}−\mathrm{bq}\right)+\left(\mathrm{3b}−\mathrm{bp}+\mathrm{aq}\right)\mathrm{i}=\mathrm{17}−\mathrm{30i} \\ $$$$\rightarrow\begin{cases}{\mathrm{3a}−\mathrm{ap}−\mathrm{bq}=\mathrm{17}}\\{\mathrm{3b}−\mathrm{bp}+\mathrm{aq}=−\mathrm{30}}\end{cases} \\ $$$$\rightarrow\begin{cases}{\mathrm{27}+\mathrm{6p}−\mathrm{9p}−\mathrm{2p}^{\mathrm{2}} −\mathrm{2q}^{\mathrm{2}} =\mathrm{17}}\\{\mathrm{6q}−\mathrm{2pq}+\mathrm{9q}+\mathrm{2pq}=−\mathrm{30}}\end{cases} \\ $$$$\rightarrow\begin{cases}{\mathrm{27}−\mathrm{3p}−\mathrm{2p}^{\mathrm{2}} −\mathrm{2q}^{\mathrm{2}} =\mathrm{17}}\\{\mathrm{15q}=−\mathrm{30},\:\mathrm{q}=−\mathrm{2}\:\mathrm{then}\:\mathrm{b}=−\mathrm{4}}\end{cases} \\ $$$$\left(\ast\right)\mathrm{27}−\mathrm{3p}−\mathrm{2p}^{\mathrm{2}} −\mathrm{8}=\mathrm{17} \\ $$$$\mathrm{2p}^{\mathrm{2}} +\mathrm{3p}−\mathrm{2}=\mathrm{0},\:\left(\mathrm{2p}−\mathrm{1}\right)\left(\mathrm{p}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\begin{cases}{\mathrm{p}=\frac{\mathrm{1}}{\mathrm{2}}\:\rightarrow\mathrm{a}=\mathrm{9}+\mathrm{1}=\mathrm{10}}\\{\mathrm{p}=−\mathrm{2}\rightarrow\mathrm{a}=\mathrm{9}−\mathrm{4}=\mathrm{5}}\end{cases} \\ $$$$\mathrm{therefore}\:\mathrm{case}\left(\mathrm{1}\right)\:\mathrm{w}=\mathrm{10}−\mathrm{4i}\:\&\:\mathrm{z}=\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2i} \\ $$$$\mathrm{case}\left(\mathrm{2}\right)\mathrm{w}=\mathrm{5}−\mathrm{4i}\:\&\:\mathrm{z}=−\mathrm{2}−\mathrm{2i} \\ $$
Commented by bemath last updated on 09/Sep/20
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *