Question Number 112795 by I want to learn more last updated on 09/Sep/20

Commented by MJS_new last updated on 10/Sep/20
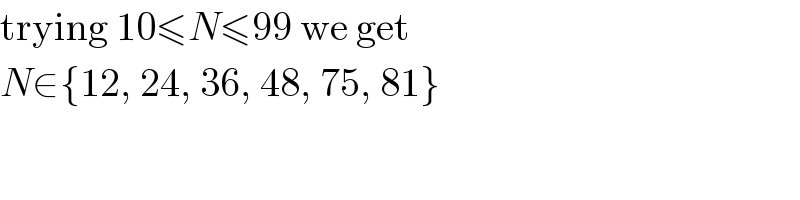
$$\mathrm{trying}\:\mathrm{10}\leqslant{N}\leqslant\mathrm{99}\:\mathrm{we}\:\mathrm{get} \\ $$$${N}\in\left\{\mathrm{12},\:\mathrm{24},\:\mathrm{36},\:\mathrm{48},\:\mathrm{75},\:\mathrm{81}\right\} \\ $$
Answered by Rasheed.Sindhi last updated on 10/Sep/20
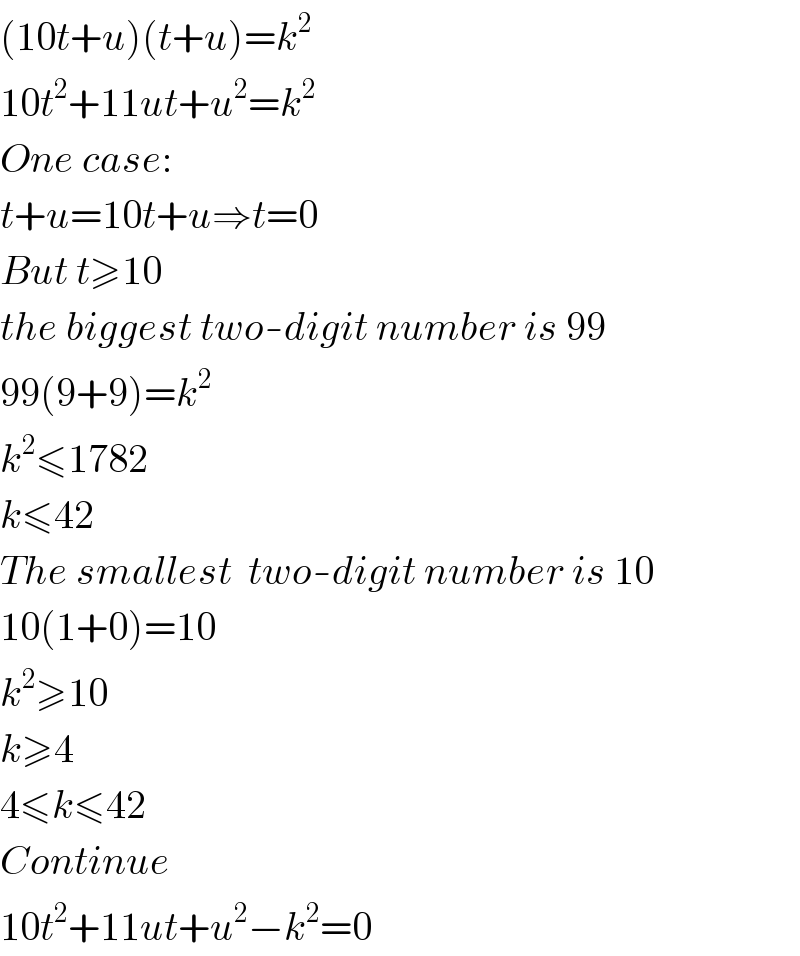
$$\left(\mathrm{10}{t}+{u}\right)\left({t}+{u}\right)={k}^{\mathrm{2}} \\ $$$$\mathrm{10}{t}^{\mathrm{2}} +\mathrm{11}{ut}+{u}^{\mathrm{2}} ={k}^{\mathrm{2}} \\ $$$${One}\:{case}: \\ $$$${t}+{u}=\mathrm{10}{t}+{u}\Rightarrow{t}=\mathrm{0} \\ $$$${But}\:{t}\geqslant\mathrm{10} \\ $$$${the}\:{biggest}\:{two}-{digit}\:{number}\:{is}\:\mathrm{99} \\ $$$$\mathrm{99}\left(\mathrm{9}+\mathrm{9}\right)={k}^{\mathrm{2}} \\ $$$${k}^{\mathrm{2}} \leqslant\mathrm{1782} \\ $$$${k}\leqslant\mathrm{42} \\ $$$${The}\:{smallest}\:\:{two}-{digit}\:{number}\:{is}\:\mathrm{10} \\ $$$$\mathrm{10}\left(\mathrm{1}+\mathrm{0}\right)=\mathrm{10} \\ $$$${k}^{\mathrm{2}} \geqslant\mathrm{10} \\ $$$${k}\geqslant\mathrm{4} \\ $$$$\mathrm{4}\leqslant{k}\leqslant\mathrm{42} \\ $$$${Continue} \\ $$$$\mathrm{10}{t}^{\mathrm{2}} +\mathrm{11}{ut}+{u}^{\mathrm{2}} −{k}^{\mathrm{2}} =\mathrm{0} \\ $$
Commented by I want to learn more last updated on 09/Sep/20
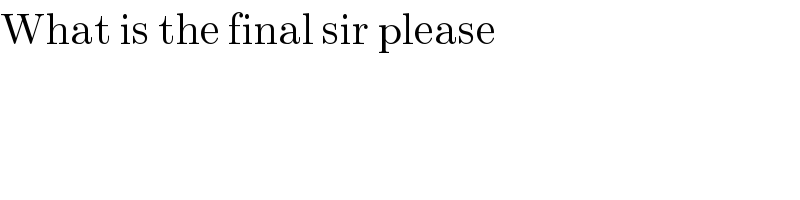
$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{final}\:\mathrm{sir}\:\mathrm{please} \\ $$
Commented by I want to learn more last updated on 11/Sep/20

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
