Question Number 112808 by Aina Samuel Temidayo last updated on 09/Sep/20
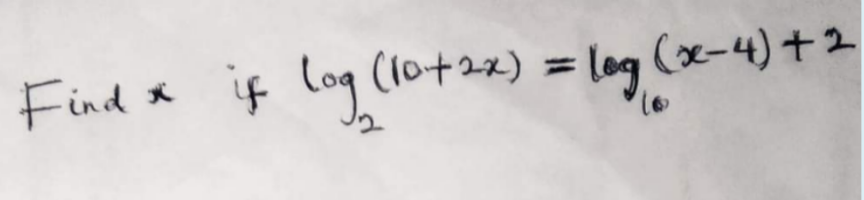
Answered by 1549442205PVT last updated on 10/Sep/20
![We have log_2 (10+2x)=log_(10) (x−4)+2 ⇔[log_2 (10+2x)−2]−log_(10) (x−4)=0(1) We need the condition x>4.Then log_2 (10+2x)−2=log_4 (10+2x)^2 −2 ≥log_4 (80x)−2=log_4 (5x)(2) (since (a+b)^2 ≥4ab⇒(10+2x)^2 ≥80x) Now we prove log_4 (5x)>log_(10) (x−4) Indeed,we have log_4 (5x)>log_(10) (5x)(3) but since x>4,so 5x>x−4.This implies that log_(10) (5x)>log_(10) (x−4)(4) From (2)(3)(4) we get log_2 (10+2x)−2>log_(10) (x−4).Hence LHS(1)>0 which means the equation has no solutions Thus,there don′t exist x satisfying the equality log_2 (10+2x)=log_(10) (x−4)+2](https://www.tinkutara.com/question/Q112899.png)
$$\mathrm{We}\:\mathrm{have}\:\mathrm{log}_{\mathrm{2}} \left(\mathrm{10}+\mathrm{2x}\right)=\mathrm{log}_{\mathrm{10}} \left(\mathrm{x}−\mathrm{4}\right)+\mathrm{2} \\ $$$$\Leftrightarrow\left[\mathrm{log}_{\mathrm{2}} \left(\mathrm{10}+\mathrm{2x}\right)−\mathrm{2}\right]−\mathrm{log}_{\mathrm{10}} \left(\mathrm{x}−\mathrm{4}\right)=\mathrm{0}\left(\mathrm{1}\right) \\ $$$$\mathrm{We}\:\mathrm{need}\:\mathrm{the}\:\mathrm{condition}\:\mathrm{x}>\mathrm{4}.\mathrm{Then} \\ $$$$\mathrm{log}_{\mathrm{2}} \left(\mathrm{10}+\mathrm{2x}\right)−\mathrm{2}=\mathrm{log}_{\mathrm{4}} \left(\mathrm{10}+\mathrm{2x}\right)^{\mathrm{2}} −\mathrm{2} \\ $$$$\geqslant\mathrm{log}_{\mathrm{4}} \left(\mathrm{80x}\right)−\mathrm{2}=\mathrm{log}_{\mathrm{4}} \left(\mathrm{5x}\right)\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{since}\:\left(\mathrm{a}+\mathrm{b}\right)^{\mathrm{2}} \geqslant\mathrm{4ab}\Rightarrow\left(\mathrm{10}+\mathrm{2x}\right)^{\mathrm{2}} \geqslant\mathrm{80x}\right) \\ $$$$\mathrm{Now}\:\mathrm{we}\:\mathrm{prove}\:\mathrm{log}_{\mathrm{4}} \left(\mathrm{5x}\right)>\mathrm{log}_{\mathrm{10}} \left(\mathrm{x}−\mathrm{4}\right) \\ $$$$\mathrm{Indeed},\mathrm{we}\:\mathrm{have}\:\mathrm{log}_{\mathrm{4}} \left(\mathrm{5x}\right)>\mathrm{log}_{\mathrm{10}} \left(\mathrm{5x}\right)\left(\mathrm{3}\right) \\ $$$$\mathrm{but}\:\mathrm{since}\:\mathrm{x}>\mathrm{4},\mathrm{so}\:\:\mathrm{5x}>\mathrm{x}−\mathrm{4}.\mathrm{This}\: \\ $$$$\mathrm{implies}\:\mathrm{that}\:\mathrm{log}_{\mathrm{10}} \left(\mathrm{5x}\right)>\mathrm{log}_{\mathrm{10}} \left(\mathrm{x}−\mathrm{4}\right)\left(\mathrm{4}\right) \\ $$$$\mathrm{From}\:\left(\mathrm{2}\right)\left(\mathrm{3}\right)\left(\mathrm{4}\right)\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{log}_{\mathrm{2}} \left(\mathrm{10}+\mathrm{2x}\right)−\mathrm{2}>\mathrm{log}_{\mathrm{10}} \left(\mathrm{x}−\mathrm{4}\right).\mathrm{Hence} \\ $$$$\mathrm{LHS}\left(\mathrm{1}\right)>\mathrm{0}\:\mathrm{which}\:\mathrm{means}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{has}\:\mathrm{no}\:\mathrm{solutions} \\ $$$$\boldsymbol{\mathrm{Thus}},\boldsymbol{\mathrm{there}}\:\boldsymbol{\mathrm{don}}'\boldsymbol{\mathrm{t}}\:\boldsymbol{\mathrm{exist}}\:\boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{satisfying}}\: \\ $$$$\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{equality}} \\ $$$$\boldsymbol{\mathrm{log}}_{\mathrm{2}} \left(\mathrm{10}+\mathrm{2}\boldsymbol{\mathrm{x}}\right)=\boldsymbol{\mathrm{log}}_{\mathrm{10}} \left(\boldsymbol{\mathrm{x}}−\mathrm{4}\right)+\mathrm{2} \\ $$
