Question Number 112818 by Algoritm last updated on 09/Sep/20
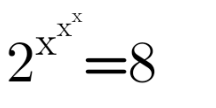
Commented by Algoritm last updated on 09/Sep/20

$$\mathrm{xlog}_{\mathrm{2}} \mathrm{2}^{\mathrm{x}^{\mathrm{x}} } =\mathrm{3}\:\:\neq\:\:\mathrm{2}^{\mathrm{x}^{\mathrm{x}^{\mathrm{x}} } } =\mathrm{8} \\ $$
Commented by Algoritm last updated on 09/Sep/20

$$\mathrm{x}^{\mathrm{x}^{\mathrm{x}} } =\mathrm{3} \\ $$
Commented by mr W last updated on 09/Sep/20
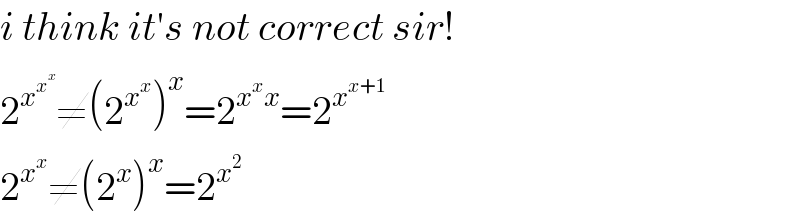
$${i}\:{think}\:{it}'{s}\:{not}\:{correct}\:{sir}! \\ $$$$\mathrm{2}^{{x}^{{x}^{{x}} } } \neq\left(\mathrm{2}^{{x}^{{x}} } \right)^{{x}} =\mathrm{2}^{{x}^{{x}} {x}} =\mathrm{2}^{{x}^{{x}+\mathrm{1}} } \\ $$$$\mathrm{2}^{{x}^{{x}} } \neq\left(\mathrm{2}^{{x}} \right)^{{x}} =\mathrm{2}^{{x}^{\mathrm{2}} } \\ $$
