Menu Close

Question-112962

Tinku Tara 0 Comments
Pin




Question Number 112962 by mohammad17 last updated on 10/Sep/20
Commented by john santu last updated on 10/Sep/20
i think ∫_0 ^∞ t^8 e^(−4t) dt
$${i}\:{think}\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\:{t}^{\mathrm{8}} \:{e}^{−\mathrm{4}{t}} \:{dt} \\ $$
Commented by Dwaipayan Shikari last updated on 10/Sep/20
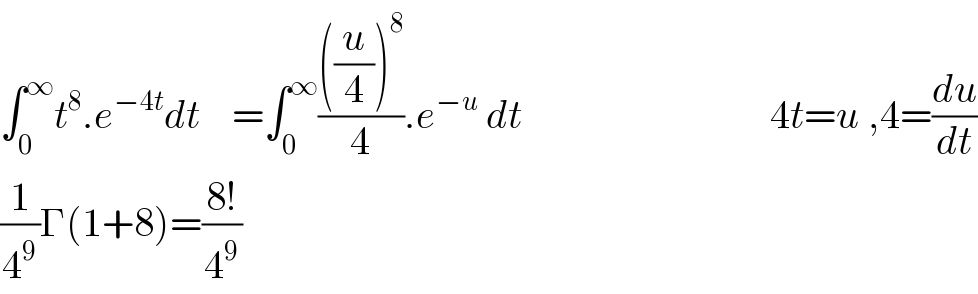
∫_0 ^∞ t^8 .e^(−4t) dt =∫_0 ^∞ ((((u/4))^8 )/4).e^(−u) dt 4t=u ,4=(du/dt) (1/4^9 )Γ(1+8)=((8!)/4^9 )
$$\int_{\mathrm{0}} ^{\infty} {t}^{\mathrm{8}} .{e}^{−\mathrm{4}{t}} {dt}\:\:\:\:=\int_{\mathrm{0}} ^{\infty} \frac{\left(\frac{{u}}{\mathrm{4}}\right)^{\mathrm{8}} }{\mathrm{4}}.{e}^{−{u}} \:{dt}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{4}{t}={u}\:,\mathrm{4}=\frac{{du}}{{dt}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{9}} }\Gamma\left(\mathrm{1}+\mathrm{8}\right)=\frac{\mathrm{8}!}{\mathrm{4}^{\mathrm{9}} } \\ $$
Commented by Aziztisffola last updated on 10/Sep/20
I think you mean ∫_0 ^( ∞) t^8 e^(−4t) dt In this case; here is the solution: let f(t)=t^8 ⇒ L{f(t)}=F(s)=((8!)/s^9 ) L {t^8 e^(−4t) }=L {f(t)e^(−4t) }=F(s+4) =((8!)/((s+4)^9 )) then ∫_0 ^( ∞) e^(−st) t^8 e^(−4t) dt=((8!)/((s+4)^9 )) let s=0 ⇒∫_0 ^( ∞) t^8 e^(−4t) dt= ((8!)/4^9 )
$$\mathrm{I}\:\mathrm{think}\:\mathrm{you}\:\mathrm{mean}\:\int_{\mathrm{0}} ^{\:\infty} \mathrm{t}^{\mathrm{8}} \mathrm{e}^{−\mathrm{4t}} \mathrm{dt} \\ $$$$\:\mathrm{In}\:\mathrm{this}\:\mathrm{case};\:\mathrm{here}\:\mathrm{is}\:\mathrm{the}\:\mathrm{solution}: \\ $$$$\:\mathrm{let}\:\mathrm{f}\left(\mathrm{t}\right)=\mathrm{t}^{\mathrm{8}} \:\:\Rightarrow\:\mathscr{L}\left\{\mathrm{f}\left(\mathrm{t}\right)\right\}=\mathrm{F}\left(\mathrm{s}\right)=\frac{\mathrm{8}!}{\mathrm{s}^{\mathrm{9}} } \\ $$$$\:\mathscr{L}\:\left\{\mathrm{t}^{\mathrm{8}} \mathrm{e}^{−\mathrm{4t}} \right\}=\mathscr{L}\:\left\{\mathrm{f}\left(\mathrm{t}\right)\mathrm{e}^{−\mathrm{4t}} \right\}=\mathrm{F}\left(\mathrm{s}+\mathrm{4}\right) \\ $$$$\:=\frac{\mathrm{8}!}{\left(\mathrm{s}+\mathrm{4}\right)^{\mathrm{9}} } \\ $$$$\:\mathrm{then}\:\int_{\mathrm{0}} ^{\:\infty} \mathrm{e}^{−\mathrm{st}} \mathrm{t}^{\mathrm{8}} \mathrm{e}^{−\mathrm{4t}} \mathrm{dt}=\frac{\mathrm{8}!}{\left(\mathrm{s}+\mathrm{4}\right)^{\mathrm{9}} } \\ $$$$\:\mathrm{let}\:\mathrm{s}=\mathrm{0}\:\Rightarrow\int_{\mathrm{0}} ^{\:\infty} \mathrm{t}^{\mathrm{8}} \mathrm{e}^{−\mathrm{4t}} \mathrm{dt}=\:\frac{\mathrm{8}!}{\mathrm{4}^{\mathrm{9}} }\: \\ $$$$\: \\ $$
Answered by Dwaipayan Shikari last updated on 10/Sep/20
x^8 ∫_0 ^∞ e^(−4t) dt (1/(−4))x^8 [e^(−4t) ]_0 ^∞ =(x^8 /4)
$${x}^{\mathrm{8}} \int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{4}{t}} {dt} \\ $$$$\frac{\mathrm{1}}{−\mathrm{4}}{x}^{\mathrm{8}} \left[{e}^{−\mathrm{4}{t}} \right]_{\mathrm{0}} ^{\infty} =\frac{{x}^{\mathrm{8}} }{\mathrm{4}} \\ $$
Commented by mohammad17 last updated on 10/Sep/20
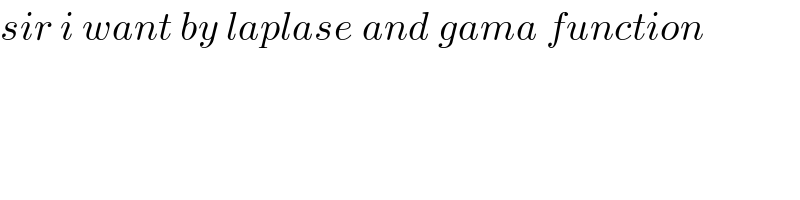
sir i want by laplase and gama function
$${sir}\:{i}\:{want}\:{by}\:{laplase}\:{and}\:{gama}\:{function} \\ $$
Answered by Aziztisffola last updated on 10/Sep/20
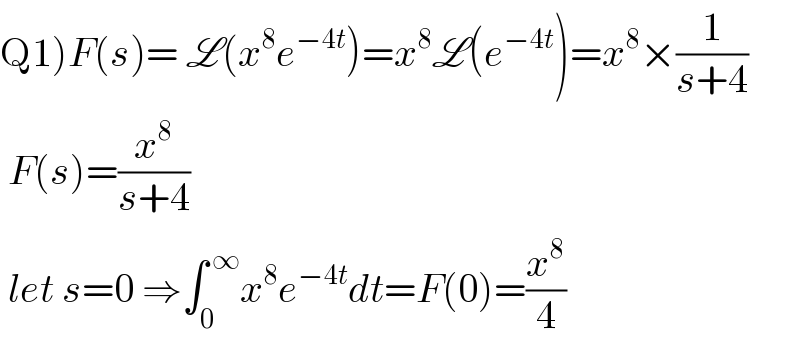
Q1)F(s)= L(x^8 e^(−4t) )=x^8 L(e^(−4t) )=x^8 ×(1/(s+4)) F(s)=(x^8 /(s+4)) let s=0 ⇒∫_0 ^( ∞) x^8 e^(−4t) dt=F(0)=(x^8 /4)
$$\left.\mathrm{Q1}\right){F}\left({s}\right)=\:\mathscr{L}\left({x}^{\mathrm{8}} {e}^{−\mathrm{4}{t}} \right)={x}^{\mathrm{8}} \mathscr{L}\left({e}^{−\mathrm{4}{t}} \right)={x}^{\mathrm{8}} ×\frac{\mathrm{1}}{{s}+\mathrm{4}} \\ $$$$\:{F}\left({s}\right)=\frac{{x}^{\mathrm{8}} }{{s}+\mathrm{4}} \\ $$$$\:{let}\:{s}=\mathrm{0}\:\Rightarrow\int_{\mathrm{0}} ^{\:\infty} {x}^{\mathrm{8}} {e}^{−\mathrm{4}{t}} {dt}={F}\left(\mathrm{0}\right)=\frac{{x}^{\mathrm{8}} }{\mathrm{4}} \\ $$
Answered by mathmax by abdo last updated on 11/Sep/20
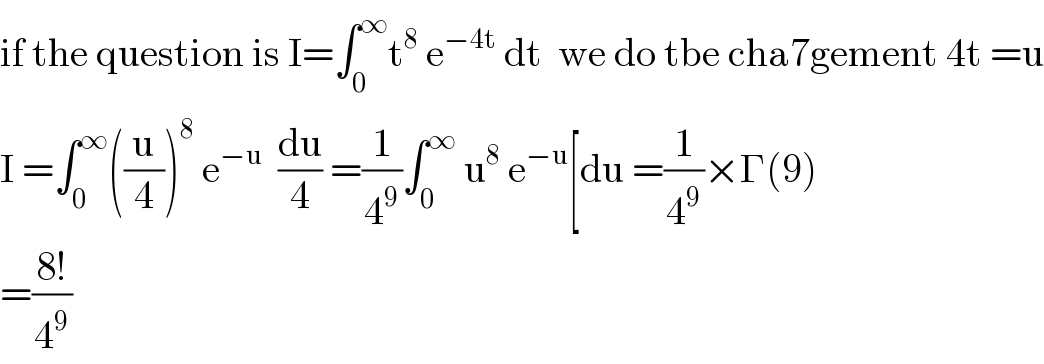
if the question is I=∫_0 ^∞ t^8 e^(−4t) dt we do tbe cha7gement 4t =u I =∫_0 ^∞ ((u/4))^8 e^(−u) (du/4) =(1/4^9 )∫_0 ^∞ u^8 e^(−u) [du =(1/4^9 )×Γ(9) =((8!)/4^9 )
$$\mathrm{if}\:\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \mathrm{t}^{\mathrm{8}} \:\mathrm{e}^{−\mathrm{4t}} \:\mathrm{dt}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{tbe}\:\mathrm{cha7gement}\:\mathrm{4t}\:=\mathrm{u} \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{u}}{\mathrm{4}}\right)^{\mathrm{8}} \:\mathrm{e}^{−\mathrm{u}} \:\:\frac{\mathrm{du}}{\mathrm{4}}\:=\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{9}} }\int_{\mathrm{0}} ^{\infty} \:\mathrm{u}^{\mathrm{8}} \:\mathrm{e}^{−\mathrm{u}} \left[\mathrm{du}\:=\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{9}} }×\Gamma\left(\mathrm{9}\right)\right. \\ $$$$=\frac{\mathrm{8}!}{\mathrm{4}^{\mathrm{9}} } \\ $$
Answered by mathmax by abdo last updated on 11/Sep/20
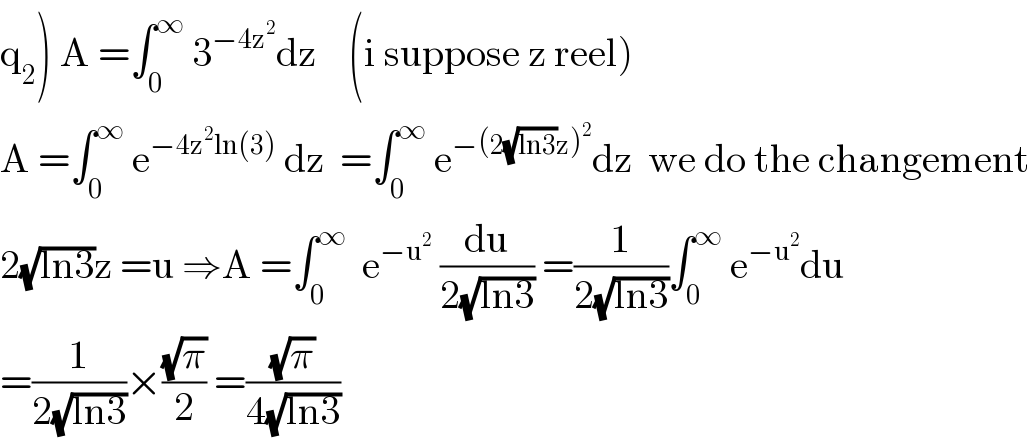
q_2 ) A =∫_0 ^∞ 3^(−4z^2 ) dz (i suppose z reel) A =∫_0 ^∞ e^(−4z^2 ln(3)) dz =∫_0 ^∞ e^(−(2(√(ln3))z)^2 ) dz we do the changement 2(√(ln3))z =u ⇒A =∫_0 ^∞ e^(−u^2 ) (du/(2(√(ln3)))) =(1/(2(√(ln3))))∫_0 ^∞ e^(−u^2 ) du =(1/(2(√(ln3))))×((√π)/2) =((√π)/(4(√(ln3))))
$$\left.\mathrm{q}_{\mathrm{2}} \right)\:\mathrm{A}\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{3}^{−\mathrm{4z}^{\mathrm{2}} } \mathrm{dz}\:\:\:\:\left(\mathrm{i}\:\mathrm{suppose}\:\mathrm{z}\:\mathrm{reel}\right) \\ $$$$\mathrm{A}\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{4z}^{\mathrm{2}} \mathrm{ln}\left(\mathrm{3}\right)} \:\mathrm{dz}\:\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{2}\sqrt{\mathrm{ln3}}\mathrm{z}\right)^{\mathrm{2}} } \mathrm{dz}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement} \\ $$$$\mathrm{2}\sqrt{\mathrm{ln3}}\mathrm{z}\:=\mathrm{u}\:\Rightarrow\mathrm{A}\:=\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{−\mathrm{u}^{\mathrm{2}} } \:\frac{\mathrm{du}}{\mathrm{2}\sqrt{\mathrm{ln3}}}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{ln3}}}\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{u}^{\mathrm{2}} } \mathrm{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{ln3}}}×\frac{\sqrt{\pi}}{\mathrm{2}}\:=\frac{\sqrt{\pi}}{\mathrm{4}\sqrt{\mathrm{ln3}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *