Menu Close

Question-112992

Tinku Tara 0 Comments
Pin




Question Number 112992 by Khanacademy last updated on 10/Sep/20
Commented by Khanacademy last updated on 10/Sep/20
(x:y)=?
$$\left(\boldsymbol{{x}}:\boldsymbol{{y}}\right)=? \\ $$
Answered by bobhans last updated on 11/Sep/20
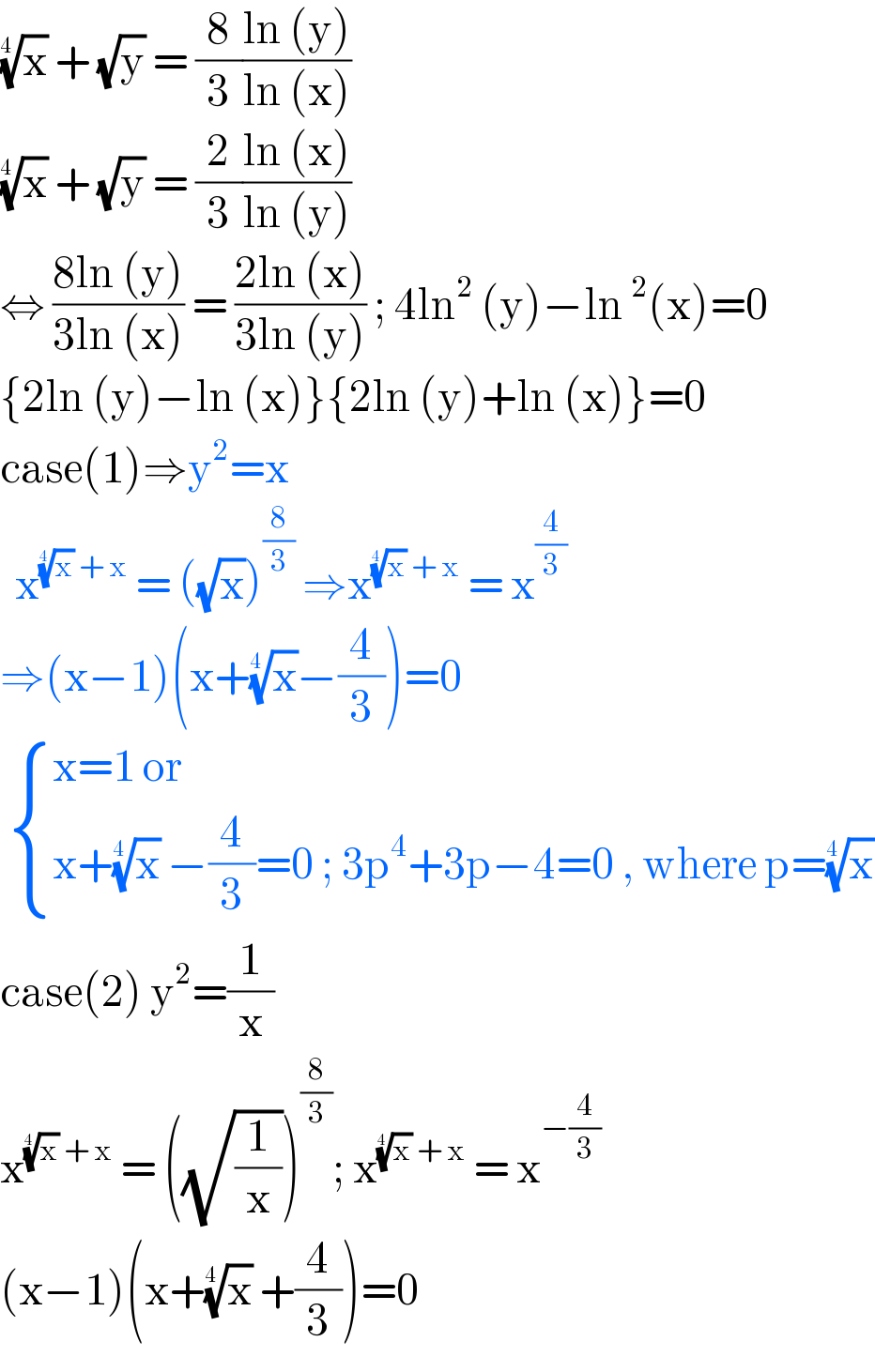
(x)^(1/(4 )) + (√y) = (8/3)((ln (y))/(ln (x))) (x)^(1/(4 )) + (√y) = (2/3)((ln (x))/(ln (y))) ⇔ ((8ln (y))/(3ln (x))) = ((2ln (x))/(3ln (y))) ; 4ln^2 (y)−ln^2 (x)=0 {2ln (y)−ln (x)}{2ln (y)+ln (x)}=0 case(1)⇒y^2 =x x^((x)^(1/(4 )) + x) = ((√x))^(8/3) ⇒x^((x)^(1/(4 )) + x) = x^(4/3) ⇒(x−1)(x+(x)^(1/(4 )) −(4/3))=0 { ((x=1 or)),((x+(x)^(1/(4 )) −(4/3)=0 ; 3p^4 +3p−4=0 , where p=(x)^(1/(4 )) )) :} case(2) y^2 =(1/x) x^((x)^(1/(4 )) + x) = ((√(1/x)))^(8/3) ; x^((x)^(1/(4 )) + x) = x^(−(4/3)) (x−1)(x+(x)^(1/(4 )) +(4/3))=0
$$\sqrt[{\mathrm{4}\:}]{\mathrm{x}}\:+\:\sqrt{\mathrm{y}}\:=\:\frac{\mathrm{8}}{\mathrm{3}}\frac{\mathrm{ln}\:\left(\mathrm{y}\right)}{\mathrm{ln}\:\left(\mathrm{x}\right)} \\ $$$$\sqrt[{\mathrm{4}\:}]{\mathrm{x}}\:+\:\sqrt{\mathrm{y}}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\frac{\mathrm{ln}\:\left(\mathrm{x}\right)}{\mathrm{ln}\:\left(\mathrm{y}\right)} \\ $$$$\Leftrightarrow\:\frac{\mathrm{8ln}\:\left(\mathrm{y}\right)}{\mathrm{3ln}\:\left(\mathrm{x}\right)}\:=\:\frac{\mathrm{2ln}\:\left(\mathrm{x}\right)}{\mathrm{3ln}\:\left(\mathrm{y}\right)}\:;\:\mathrm{4ln}^{\mathrm{2}} \:\left(\mathrm{y}\right)−\mathrm{ln}\:^{\mathrm{2}} \left(\mathrm{x}\right)=\mathrm{0} \\ $$$$\left\{\mathrm{2ln}\:\left(\mathrm{y}\right)−\mathrm{ln}\:\left(\mathrm{x}\right)\right\}\left\{\mathrm{2ln}\:\left(\mathrm{y}\right)+\mathrm{ln}\:\left(\mathrm{x}\right)\right\}=\mathrm{0} \\ $$$$\mathrm{case}\left(\mathrm{1}\right)\Rightarrow\mathrm{y}^{\mathrm{2}} =\mathrm{x} \\ $$$$\:\:\mathrm{x}^{\sqrt[{\mathrm{4}\:}]{\mathrm{x}}\:+\:\mathrm{x}} \:=\:\left(\sqrt{\mathrm{x}}\right)^{\frac{\mathrm{8}}{\mathrm{3}}} \:\Rightarrow\mathrm{x}^{\sqrt[{\mathrm{4}\:}]{\mathrm{x}}\:+\:\mathrm{x}} \:=\:\mathrm{x}^{\frac{\mathrm{4}}{\mathrm{3}}} \\ $$$$\Rightarrow\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}+\sqrt[{\mathrm{4}\:}]{\mathrm{x}}−\frac{\mathrm{4}}{\mathrm{3}}\right)=\mathrm{0} \\ $$$$\:\begin{cases}{\mathrm{x}=\mathrm{1}\:\mathrm{or}}\\{\mathrm{x}+\sqrt[{\mathrm{4}\:}]{\mathrm{x}}\:−\frac{\mathrm{4}}{\mathrm{3}}=\mathrm{0}\:;\:\mathrm{3p}^{\mathrm{4}} +\mathrm{3p}−\mathrm{4}=\mathrm{0}\:,\:\mathrm{where}\:\mathrm{p}=\sqrt[{\mathrm{4}\:}]{\mathrm{x}}}\end{cases} \\ $$$$\mathrm{case}\left(\mathrm{2}\right)\:\mathrm{y}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{x}} \\ $$$$\mathrm{x}^{\sqrt[{\mathrm{4}\:}]{\mathrm{x}}\:+\:\mathrm{x}} \:=\:\left(\sqrt{\frac{\mathrm{1}}{\mathrm{x}}}\right)^{\frac{\mathrm{8}}{\mathrm{3}}} ;\:\mathrm{x}^{\sqrt[{\mathrm{4}\:}]{\mathrm{x}}\:+\:\mathrm{x}} \:=\:\mathrm{x}^{−\frac{\mathrm{4}}{\mathrm{3}}} \\ $$$$\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}+\sqrt[{\mathrm{4}\:}]{\mathrm{x}}\:+\frac{\mathrm{4}}{\mathrm{3}}\right)=\mathrm{0} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *