Menu Close

Question-113109

Tinku Tara 0 Comments
Pin




Question Number 113109 by bemath last updated on 11/Sep/20
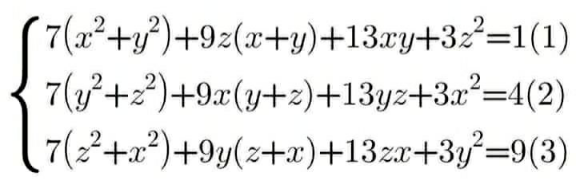
Commented by bemath last updated on 11/Sep/20
any one help this question?
$$\mathrm{any}\:\mathrm{one}\:\mathrm{help}\:\mathrm{this}\:\mathrm{question}? \\ $$
Commented by bemath last updated on 11/Sep/20
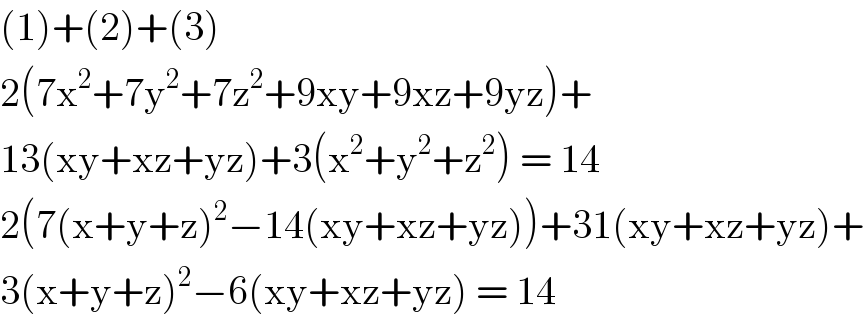
(1)+(2)+(3) 2(7x^2 +7y^2 +7z^2 +9xy+9xz+9yz)+ 13(xy+xz+yz)+3(x^2 +y^2 +z^2 ) = 14 2(7(x+y+z)^2 −14(xy+xz+yz))+31(xy+xz+yz)+ 3(x+y+z)^2 −6(xy+xz+yz) = 14
$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right)+\left(\mathrm{3}\right) \\ $$$$\mathrm{2}\left(\mathrm{7x}^{\mathrm{2}} +\mathrm{7y}^{\mathrm{2}} +\mathrm{7z}^{\mathrm{2}} +\mathrm{9xy}+\mathrm{9xz}+\mathrm{9yz}\right)+ \\ $$$$\mathrm{13}\left(\mathrm{xy}+\mathrm{xz}+\mathrm{yz}\right)+\mathrm{3}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} \right)\:=\:\mathrm{14} \\ $$$$\mathrm{2}\left(\mathrm{7}\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)^{\mathrm{2}} −\mathrm{14}\left(\mathrm{xy}+\mathrm{xz}+\mathrm{yz}\right)\right)+\mathrm{31}\left(\mathrm{xy}+\mathrm{xz}+\mathrm{yz}\right)+ \\ $$$$\mathrm{3}\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)^{\mathrm{2}} −\mathrm{6}\left(\mathrm{xy}+\mathrm{xz}+\mathrm{yz}\right)\:=\:\mathrm{14} \\ $$
Answered by MJS_new last updated on 11/Sep/20
(iii)−(ii) 4(x−y)z+4(x^2 −y^2 )=5 ⇒ z=−((4x^2 −4y^2 −5)/(4(x−y))) { ((16x^4 −16x^3 y−16xy^3 +16y^4 +44x^2 +32xy−76y^2 +75=0)),((16x^4 −16x^3 y−16xy^3 +16y^4 +164x^2 +208xy−44y^2 +175=0)),((z=−((4x^2 −4y^2 −5)/(4(x−y))))) :} (i)−(ii) 52x^2 −44xy−8y^2 −25=0 let x=u−v∧y=u+v 88v^2 −120uv−25=0 ⇒ u=((88v^2 −25)/(120v)) insert in (i) or (ii) v^4 −((25v^2 )/(14))+((625)/(784))=0 (28v^2 −25)^2 =0 ⇒ v=±((5(√7))/(14)) ⇒ u=±((5(√7))/(28)) ⇒ (x∣y∣z)=±(−((5(√7))/(28))∣((15(√7))/(28))∣−((17(√7))/(28)))
$$\left(\mathrm{iii}\right)−\left(\mathrm{ii}\right) \\ $$$$\mathrm{4}\left({x}−{y}\right){z}+\mathrm{4}\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)=\mathrm{5} \\ $$$$\Rightarrow\:{z}=−\frac{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{y}^{\mathrm{2}} −\mathrm{5}}{\mathrm{4}\left({x}−{y}\right)} \\ $$$$\begin{cases}{\mathrm{16}{x}^{\mathrm{4}} −\mathrm{16}{x}^{\mathrm{3}} {y}−\mathrm{16}{xy}^{\mathrm{3}} +\mathrm{16}{y}^{\mathrm{4}} +\mathrm{44}{x}^{\mathrm{2}} +\mathrm{32}{xy}−\mathrm{76}{y}^{\mathrm{2}} +\mathrm{75}=\mathrm{0}}\\{\mathrm{16}{x}^{\mathrm{4}} −\mathrm{16}{x}^{\mathrm{3}} {y}−\mathrm{16}{xy}^{\mathrm{3}} +\mathrm{16}{y}^{\mathrm{4}} +\mathrm{164}{x}^{\mathrm{2}} +\mathrm{208}{xy}−\mathrm{44}{y}^{\mathrm{2}} +\mathrm{175}=\mathrm{0}}\\{{z}=−\frac{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{y}^{\mathrm{2}} −\mathrm{5}}{\mathrm{4}\left({x}−{y}\right)}}\end{cases} \\ $$$$\left(\mathrm{i}\right)−\left(\mathrm{ii}\right) \\ $$$$\mathrm{52}{x}^{\mathrm{2}} −\mathrm{44}{xy}−\mathrm{8}{y}^{\mathrm{2}} −\mathrm{25}=\mathrm{0} \\ $$$$\mathrm{let}\:{x}={u}−{v}\wedge{y}={u}+{v} \\ $$$$\mathrm{88}{v}^{\mathrm{2}} −\mathrm{120}{uv}−\mathrm{25}=\mathrm{0} \\ $$$$\Rightarrow\:{u}=\frac{\mathrm{88}{v}^{\mathrm{2}} −\mathrm{25}}{\mathrm{120}{v}} \\ $$$$\mathrm{insert}\:\mathrm{in}\:\left(\mathrm{i}\right)\:\mathrm{or}\:\left(\mathrm{ii}\right) \\ $$$${v}^{\mathrm{4}} −\frac{\mathrm{25}{v}^{\mathrm{2}} }{\mathrm{14}}+\frac{\mathrm{625}}{\mathrm{784}}=\mathrm{0} \\ $$$$\left(\mathrm{28}{v}^{\mathrm{2}} −\mathrm{25}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\:{v}=\pm\frac{\mathrm{5}\sqrt{\mathrm{7}}}{\mathrm{14}} \\ $$$$\Rightarrow\:{u}=\pm\frac{\mathrm{5}\sqrt{\mathrm{7}}}{\mathrm{28}} \\ $$$$\Rightarrow\:\left({x}\mid{y}\mid{z}\right)=\pm\left(−\frac{\mathrm{5}\sqrt{\mathrm{7}}}{\mathrm{28}}\mid\frac{\mathrm{15}\sqrt{\mathrm{7}}}{\mathrm{28}}\mid−\frac{\mathrm{17}\sqrt{\mathrm{7}}}{\mathrm{28}}\right) \\ $$
Commented by bemath last updated on 11/Sep/20
waw....i′m stuck sir
$$\mathrm{waw}….\mathrm{i}'\mathrm{m}\:\mathrm{stuck}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *