Question Number 113114 by bemath last updated on 11/Sep/20
Commented by bemath last updated on 11/Sep/20

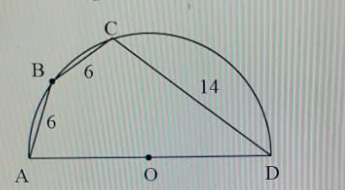
$$\mathrm{find}\:\mathrm{AD} \\ $$
Answered by mr W last updated on 11/Sep/20
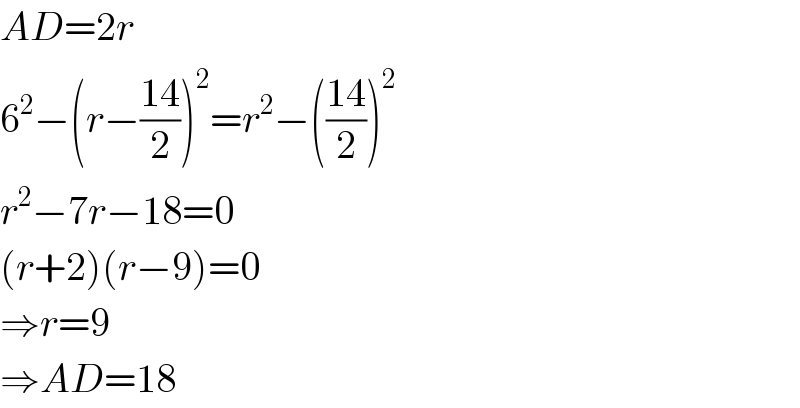
$${AD}=\mathrm{2}{r} \\ $$$$\mathrm{6}^{\mathrm{2}} −\left({r}−\frac{\mathrm{14}}{\mathrm{2}}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} −\left(\frac{\mathrm{14}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$${r}^{\mathrm{2}} −\mathrm{7}{r}−\mathrm{18}=\mathrm{0} \\ $$$$\left({r}+\mathrm{2}\right)\left({r}−\mathrm{9}\right)=\mathrm{0} \\ $$$$\Rightarrow{r}=\mathrm{9} \\ $$$$\Rightarrow{AD}=\mathrm{18} \\ $$
Commented by bemath last updated on 11/Sep/20
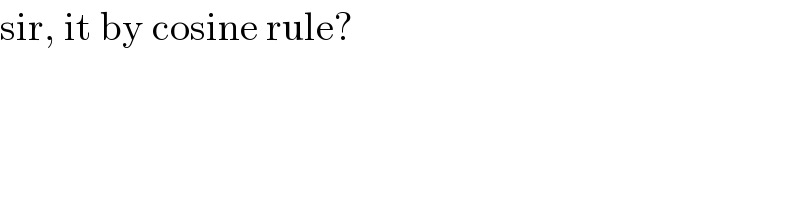
$$\mathrm{sir},\:\mathrm{it}\:\mathrm{by}\:\mathrm{cosine}\:\mathrm{rule}? \\ $$
Commented by mr W last updated on 11/Sep/20
Commented by mr W last updated on 11/Sep/20
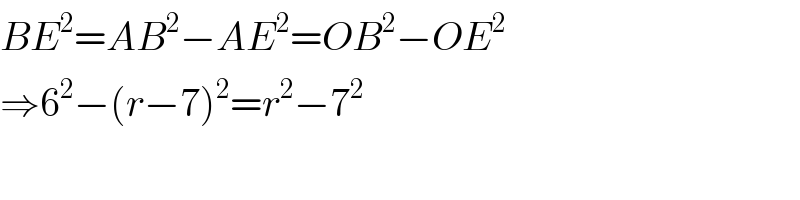
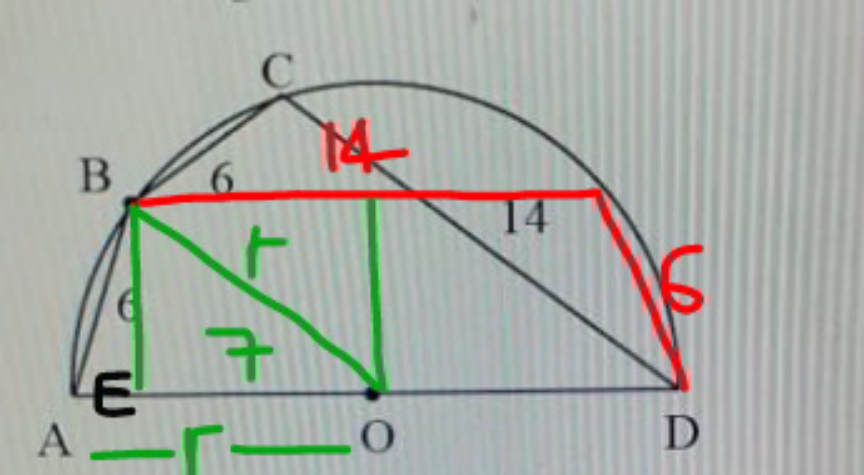
$${BE}^{\mathrm{2}} ={AB}^{\mathrm{2}} −{AE}^{\mathrm{2}} ={OB}^{\mathrm{2}} −{OE}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{6}^{\mathrm{2}} −\left({r}−\mathrm{7}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} −\mathrm{7}^{\mathrm{2}} \\ $$
Commented by bemath last updated on 11/Sep/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
