Question Number 113160 by mohammad17 last updated on 11/Sep/20

Commented by abdomsup last updated on 11/Sep/20
![not correct Γ is defined on]0,∞[](https://www.tinkutara.com/question/Q113179.png)
$$\left.{not}\:{correct}\:\Gamma\:{is}\:{defined}\:{on}\right]\mathrm{0},\infty\left[\right. \\ $$
Commented by mohammad17 last updated on 11/Sep/20
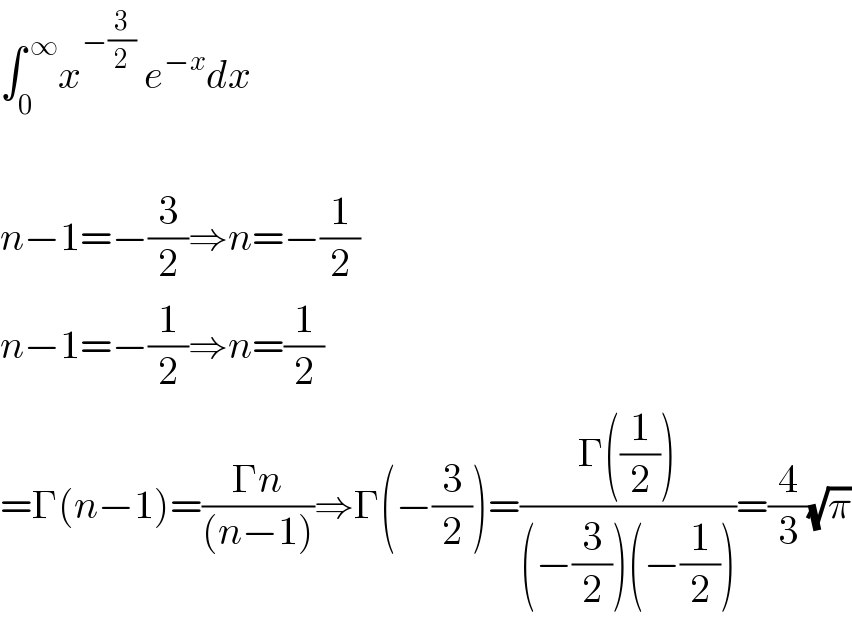
$$\int_{\mathrm{0}} ^{\:\infty} {x}^{−\frac{\mathrm{3}}{\mathrm{2}}} \:{e}^{−{x}} {dx} \\ $$$$ \\ $$$${n}−\mathrm{1}=−\frac{\mathrm{3}}{\mathrm{2}}\Rightarrow{n}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${n}−\mathrm{1}=−\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow{n}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$=\Gamma\left({n}−\mathrm{1}\right)=\frac{\Gamma{n}}{\left({n}−\mathrm{1}\right)}\Rightarrow\Gamma\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)}=\frac{\mathrm{4}}{\mathrm{3}}\sqrt{\pi} \\ $$
Commented by mohammad17 last updated on 11/Sep/20
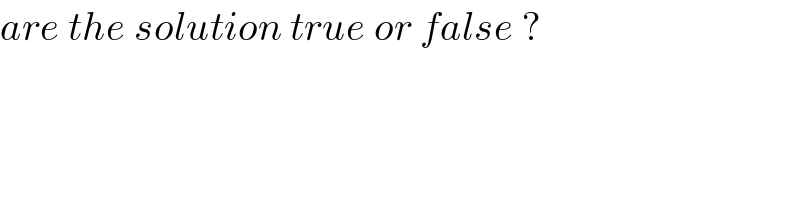
$${are}\:{the}\:{solution}\:{true}\:{or}\:{false}\:? \\ $$
Commented by 1549442205PVT last updated on 11/Sep/20
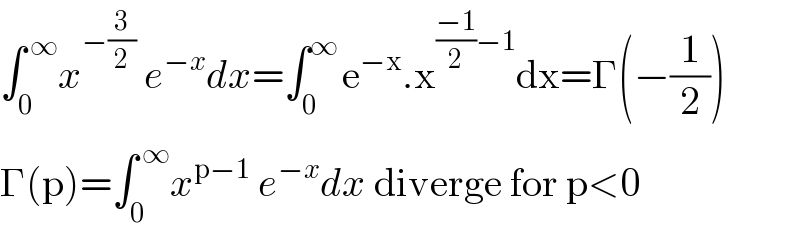
$$\int_{\mathrm{0}} ^{\:\infty} {x}^{−\frac{\mathrm{3}}{\mathrm{2}}} \:{e}^{−{x}} {dx}=\int_{\mathrm{0}} ^{\infty\:} \mathrm{e}^{−\mathrm{x}} .\mathrm{x}^{\frac{−\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \mathrm{dx}=\Gamma\left(−\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\Gamma\left(\mathrm{p}\right)=\int_{\mathrm{0}} ^{\:\infty} {x}^{\mathrm{p}−\mathrm{1}} \:{e}^{−{x}} {dx}\:\mathrm{diverge}\:\mathrm{for}\:\mathrm{p}<\mathrm{0} \\ $$
Answered by abdomsup last updated on 11/Sep/20
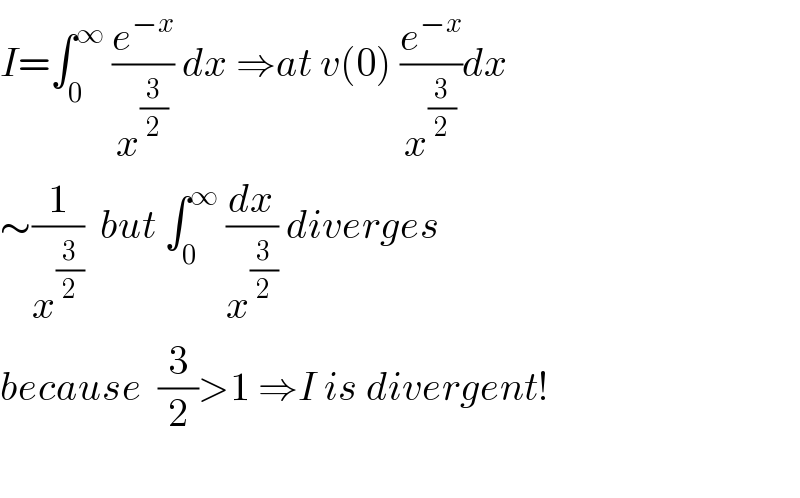
$${I}=\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−{x}} }{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }\:{dx}\:\Rightarrow{at}\:{v}\left(\mathrm{0}\right)\:\frac{{e}^{−{x}} }{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }{dx} \\ $$$$\sim\frac{\mathrm{1}}{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }\:\:{but}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{dx}}{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }\:{diverges}\: \\ $$$${because}\:\:\frac{\mathrm{3}}{\mathrm{2}}>\mathrm{1}\:\Rightarrow{I}\:{is}\:{divergent}! \\ $$$$ \\ $$
Answered by MJS_new last updated on 11/Sep/20
![∫x^q e^(−x) dx= [t=x^(q+1) → dx=(x^(−q) /(q+1))dt] =(1/(q+1))∫e^(−t^(1/(q+1)) ) dt= [incomplete Gamma−function] =(1/(q+1))(−(q+1)Γ (q+1∣t^(1/(q+1)) ))= =−Γ (q+1∣t^(1/(q+1)) )= =−Γ (q+1∣x) +C](https://www.tinkutara.com/question/Q113186.png)
$$\int{x}^{{q}} \mathrm{e}^{−{x}} {dx}= \\ $$$$\:\:\:\:\:\left[{t}={x}^{{q}+\mathrm{1}} \:\rightarrow\:{dx}=\frac{{x}^{−{q}} }{{q}+\mathrm{1}}{dt}\right] \\ $$$$=\frac{\mathrm{1}}{{q}+\mathrm{1}}\int\mathrm{e}^{−{t}^{\frac{\mathrm{1}}{{q}+\mathrm{1}}} } {dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{incomplete}\:\mathrm{Gamma}−\mathrm{function}\right] \\ $$$$=\frac{\mathrm{1}}{{q}+\mathrm{1}}\left(−\left({q}+\mathrm{1}\right)\Gamma\:\left({q}+\mathrm{1}\mid{t}^{\frac{\mathrm{1}}{{q}+\mathrm{1}}} \right)\right)= \\ $$$$=−\Gamma\:\left({q}+\mathrm{1}\mid{t}^{\frac{\mathrm{1}}{{q}+\mathrm{1}}} \right)= \\ $$$$=−\Gamma\:\left({q}+\mathrm{1}\mid{x}\right)\:+{C} \\ $$
