Question Number 113185 by 175mohamed last updated on 11/Sep/20

Answered by mindispower last updated on 12/Sep/20
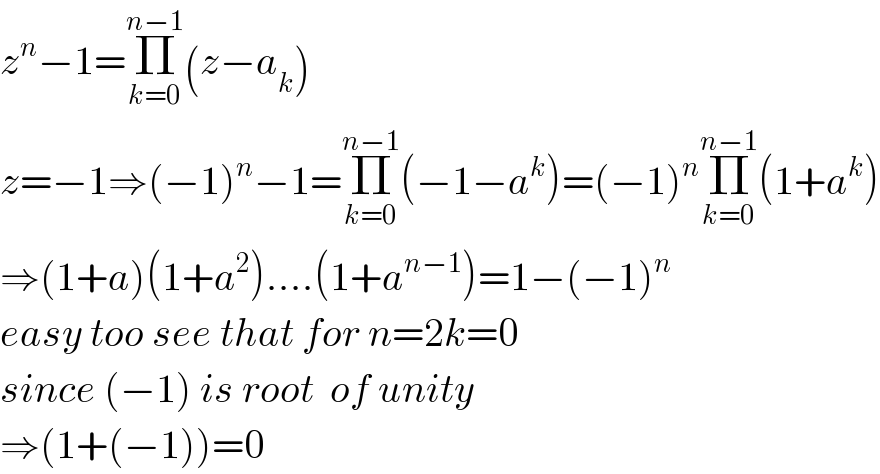
$${z}^{{n}} −\mathrm{1}=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left({z}−{a}_{{k}} \right) \\ $$$${z}=−\mathrm{1}\Rightarrow\left(−\mathrm{1}\right)^{{n}} −\mathrm{1}=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left(−\mathrm{1}−{a}^{{k}} \right)=\left(−\mathrm{1}\right)^{{n}} \underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left(\mathrm{1}+{a}^{{k}} \right) \\ $$$$\Rightarrow\left(\mathrm{1}+{a}\right)\left(\mathrm{1}+{a}^{\mathrm{2}} \right)….\left(\mathrm{1}+{a}^{{n}−\mathrm{1}} \right)=\mathrm{1}−\left(−\mathrm{1}\right)^{{n}} \\ $$$${easy}\:{too}\:{see}\:{that}\:{for}\:{n}=\mathrm{2}{k}=\mathrm{0} \\ $$$${since}\:\left(−\mathrm{1}\right)\:{is}\:{root}\:\:{of}\:{unity} \\ $$$$\Rightarrow\left(\mathrm{1}+\left(−\mathrm{1}\right)\right)=\mathrm{0} \\ $$
