Menu Close

Question-113243

Tinku Tara 0 Comments
Pin




Question Number 113243 by ShakaLaka last updated on 11/Sep/20
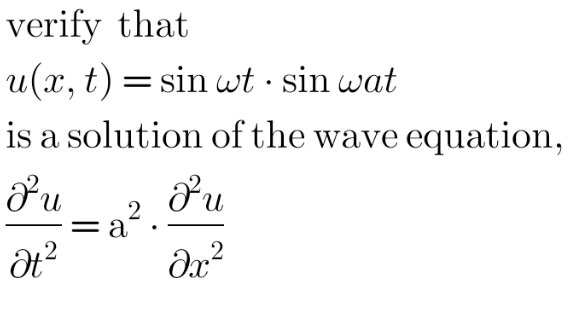
Commented by ShakaLaka last updated on 11/Sep/20
Can anybody solve this question?
$$\mathrm{Can}\:\mathrm{anybody}\:\mathrm{solve}\:\mathrm{this} \\ $$$$\mathrm{question}? \\ $$
Commented by mr W last updated on 11/Sep/20
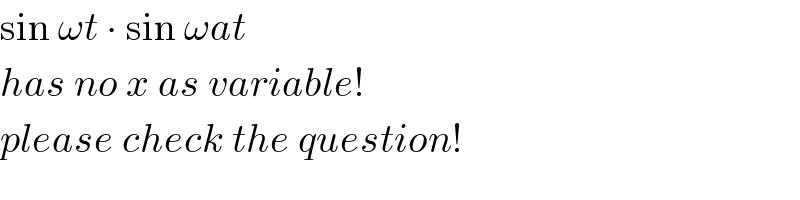
sin ωt ∙ sin ωat has no x as variable! please check the question!
$$\mathrm{sin}\:\omega{t}\:\centerdot\:\mathrm{sin}\:\omega{at} \\ $$$${has}\:{no}\:{x}\:{as}\:{variable}! \\ $$$${please}\:{check}\:{the}\:{question}! \\ $$
Commented by ShakaLaka last updated on 11/Sep/20
I will have to ask my teacher that what is the correct question. because this question I wrote is totally same as it is. Actually, this is the question of the assignmemt, which was written directly from university, not by my teacher. By the way, there is also another mistake in the question that there is written (∂^2 v/∂c^2 ) instead of (∂^2 v/∂t^2 )
$$\mathrm{I}\:\mathrm{will}\:\mathrm{have}\:\mathrm{to}\:\mathrm{ask}\:\mathrm{my}\:\mathrm{teacher} \\ $$$${that}\:{what}\:{is}\:{the}\:{correct}\:{question}. \\ $$$$\mathrm{because}\:\mathrm{this}\:\mathrm{question}\:\mathrm{I}\:\mathrm{wrote}\:\mathrm{is} \\ $$$$\mathrm{totally}\:\mathrm{same}\:\mathrm{as}\:\mathrm{it}\:\mathrm{is}. \\ $$$$\mathrm{Actually},\:\mathrm{this}\:\mathrm{is}\:\mathrm{the}\:\mathrm{question}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{assignmemt},\:{which}\:{was} \\ $$$${written}\:{directly}\:{from}\:{university}, \\ $$$${not}\:{by}\:{my}\:{teacher}. \\ $$$${By}\:{the}\:{way},\:{there}\:{is}\:{also} \\ $$$${another}\:{mistake}\:{in}\:{the}\:{question} \\ $$$${that}\:{there}\:{is}\:{written}\:\frac{\partial^{\mathrm{2}} {v}}{\partial{c}^{\mathrm{2}} }\:{instead} \\ $$$${of}\:\frac{\partial^{\mathrm{2}} {v}}{\partial{t}^{\mathrm{2}} } \\ $$
Answered by mathdave last updated on 12/Sep/20
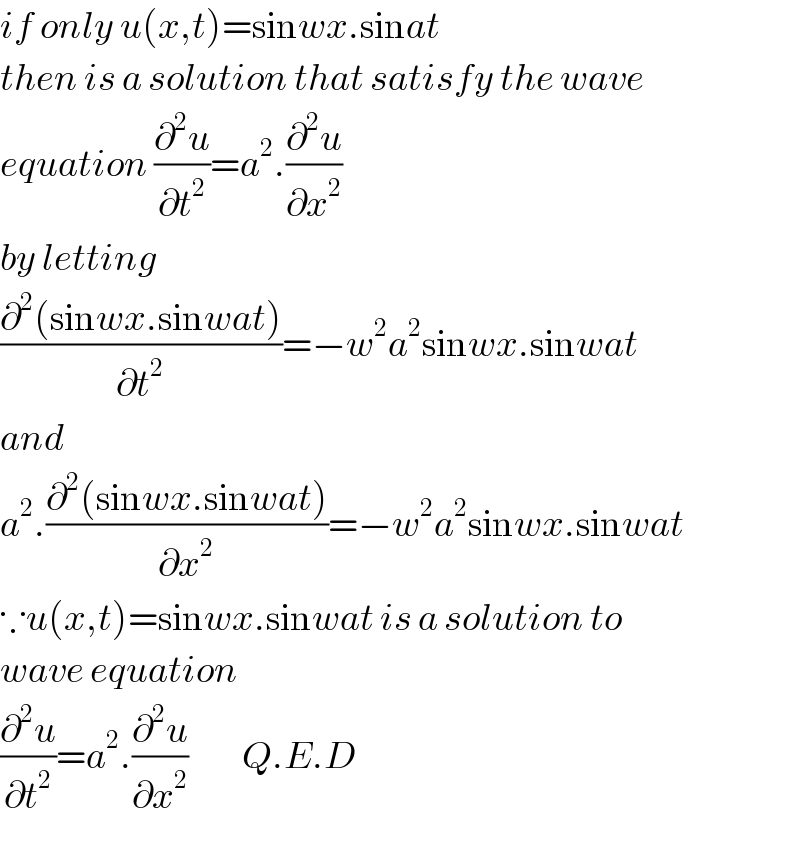
if only u(x,t)=sinwx.sinat then is a solution that satisfy the wave equation (∂^2 u/∂t^2 )=a^2 .(∂^2 u/∂x^2 ) by letting ((∂^2 (sinwx.sinwat))/∂t^2 )=−w^2 a^2 sinwx.sinwat and a^2 .((∂^2 (sinwx.sinwat))/∂x^2 )=−w^2 a^2 sinwx.sinwat ∵u(x,t)=sinwx.sinwat is a solution to wave equation (∂^2 u/∂t^2 )=a^2 .(∂^2 u/∂x^2 ) Q.E.D
$${if}\:{only}\:{u}\left({x},{t}\right)=\mathrm{sin}{wx}.\mathrm{sin}{at} \\ $$$${then}\:{is}\:{a}\:{solution}\:{that}\:{satisfy}\:{the}\:{wave} \\ $$$${equation}\:\frac{\partial^{\mathrm{2}} {u}}{\partial{t}^{\mathrm{2}} }={a}^{\mathrm{2}} .\frac{\partial^{\mathrm{2}} {u}}{\partial{x}^{\mathrm{2}} } \\ $$$${by}\:{letting} \\ $$$$\frac{\partial^{\mathrm{2}} \left(\mathrm{sin}{wx}.\mathrm{sin}{wat}\right)}{\partial{t}^{\mathrm{2}} }=−{w}^{\mathrm{2}} {a}^{\mathrm{2}} \mathrm{sin}{wx}.\mathrm{sin}{wat} \\ $$$${and} \\ $$$${a}^{\mathrm{2}} .\frac{\partial^{\mathrm{2}} \left(\mathrm{sin}{wx}.\mathrm{sin}{wat}\right)}{\partial{x}^{\mathrm{2}} }=−{w}^{\mathrm{2}} {a}^{\mathrm{2}} \mathrm{sin}{wx}.\mathrm{sin}{wat} \\ $$$$\because{u}\left({x},{t}\right)=\mathrm{sin}{wx}.\mathrm{sin}{wat}\:{is}\:{a}\:{solution}\:{to} \\ $$$${wave}\:{equation}\: \\ $$$$\frac{\partial^{\mathrm{2}} {u}}{\partial{t}^{\mathrm{2}} }={a}^{\mathrm{2}} .\frac{\partial^{\mathrm{2}} {u}}{\partial{x}^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:{Q}.{E}.{D} \\ $$
Commented by ShakaLaka last updated on 13/Sep/20
yeah mathdave, it can be possible
$${yeah}\:{mathdave},\:{it}\:{can}\:{be} \\ $$$${possible} \\ $$
Commented by ShakaLaka last updated on 15/Sep/20
mathdave you were right. my teacher is also saying that the function “sin ωt ∙ sin ωat” is incorrect, the correct function is “sin ωx ∙ sin ωat”; as you said.
$${mathdave}\:{you}\:{were}\:{right}.\:{my} \\ $$$${teacher}\:{is}\:{also}\:{saying}\:{that}\:{the} \\ $$$${function}\:“\mathrm{sin}\:\omega{t}\:\centerdot\:\mathrm{sin}\:\omega{a}\mathrm{t}''\:{is} \\ $$$${incorrect},\:{the}\:{correct}\:{function} \\ $$$${is}\:“\mathrm{sin}\:\omega{x}\:\centerdot\:\mathrm{sin}\:\omega{a}\mathrm{t}'';\:{as}\:{you}\:{said}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *