Question Number 113309 by Hassen_Timol last updated on 12/Sep/20
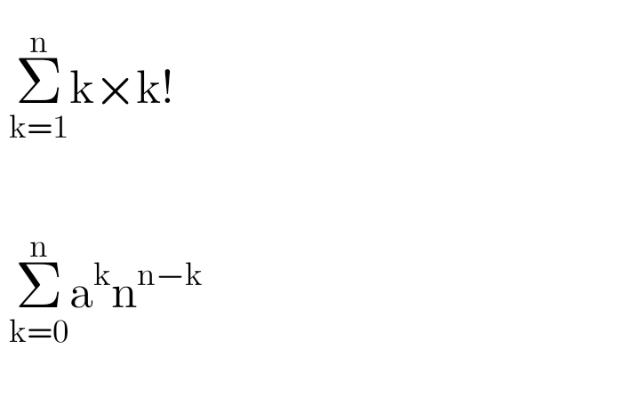
Commented by Hassen_Timol last updated on 12/Sep/20
$$\mathrm{Can}\:\mathrm{you}\:\mathrm{please}\:\mathrm{help}\:\mathrm{me}…\:? \\ $$
Commented by mathmax by abdo last updated on 12/Sep/20
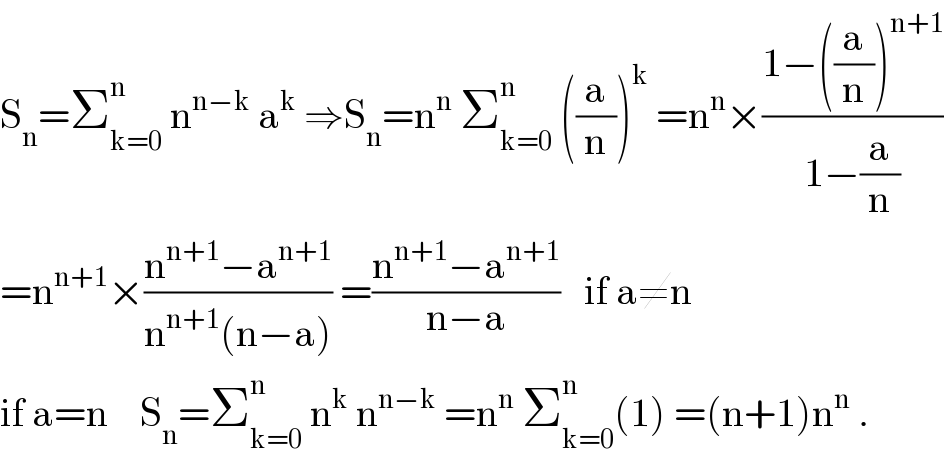
$$\mathrm{S}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}\:} \:\mathrm{n}^{\mathrm{n}−\mathrm{k}} \:\mathrm{a}^{\mathrm{k}} \:\Rightarrow\mathrm{S}_{\mathrm{n}} =\mathrm{n}^{\mathrm{n}} \:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\left(\frac{\mathrm{a}}{\mathrm{n}}\right)^{\mathrm{k}} \:=\mathrm{n}^{\mathrm{n}} ×\frac{\mathrm{1}−\left(\frac{\mathrm{a}}{\mathrm{n}}\right)^{\mathrm{n}+\mathrm{1}} }{\mathrm{1}−\frac{\mathrm{a}}{\mathrm{n}}} \\ $$$$=\mathrm{n}^{\mathrm{n}+\mathrm{1}} ×\frac{\mathrm{n}^{\mathrm{n}+\mathrm{1}} −\mathrm{a}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}^{\mathrm{n}+\mathrm{1}} \left(\mathrm{n}−\mathrm{a}\right)}\:=\frac{\mathrm{n}^{\mathrm{n}+\mathrm{1}} −\mathrm{a}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}−\mathrm{a}}\:\:\:\mathrm{if}\:\mathrm{a}\neq\mathrm{n} \\ $$$$\mathrm{if}\:\mathrm{a}=\mathrm{n}\:\:\:\:\mathrm{S}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{n}^{\mathrm{k}} \:\mathrm{n}^{\mathrm{n}−\mathrm{k}} \:=\mathrm{n}^{\mathrm{n}} \:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \left(\mathrm{1}\right)\:=\left(\mathrm{n}+\mathrm{1}\right)\mathrm{n}^{\mathrm{n}} \:. \\ $$
Commented by Hassen_Timol last updated on 12/Sep/20
Thank you so much Sir
Commented by abdomsup last updated on 12/Sep/20

$${you}\:{are}\:{welcome} \\ $$
Answered by Dwaipayan Shikari last updated on 12/Sep/20

$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}.{k}!=\mathrm{1}.\mathrm{1}!+\mathrm{2}.\mathrm{2}!+…. \\ $$$$\mathrm{1}.\mathrm{1}!=\left(\mathrm{2}−\mathrm{1}\right)\mathrm{1}!=\mathrm{2}!−\mathrm{1}! \\ $$$$\mathrm{2}.\mathrm{2}!=\mathrm{3}.\mathrm{2}!−\mathrm{2}!=\mathrm{3}!−\mathrm{2}! \\ $$$$…. \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}{k}.{k}!=\mathrm{2}!−\mathrm{1}!+\mathrm{3}!−\mathrm{2}!+\mathrm{4}!−\mathrm{3}!+…..{n}!−\left({n}−\mathrm{1}\right)!+\left({n}+\mathrm{1}\right)!−{n}! \\ $$$$=\left({n}+\mathrm{1}\right)!−\mathrm{1} \\ $$
Answered by Dwaipayan Shikari last updated on 12/Sep/20
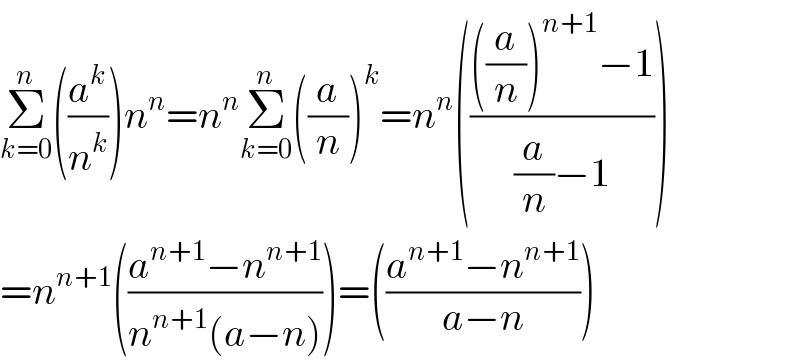
$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left(\frac{{a}^{{k}} }{{n}^{{k}} }\right){n}^{{n}} ={n}^{{n}} \underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left(\frac{{a}}{{n}}\right)^{{k}} ={n}^{{n}} \left(\frac{\left(\frac{{a}}{{n}}\right)^{{n}+\mathrm{1}} −\mathrm{1}}{\frac{{a}}{{n}}−\mathrm{1}}\right) \\ $$$$={n}^{{n}+\mathrm{1}} \left(\frac{{a}^{{n}+\mathrm{1}} −{n}^{{n}+\mathrm{1}} }{{n}^{{n}+\mathrm{1}} \left({a}−{n}\right)}\right)=\left(\frac{{a}^{{n}+\mathrm{1}} −{n}^{{n}+\mathrm{1}} }{{a}−{n}}\right) \\ $$
Commented by Hassen_Timol last updated on 12/Sep/20
Thank you so much
