Question Number 113408 by ZiYangLee last updated on 13/Sep/20

Commented by ZiYangLee last updated on 13/Sep/20

$$\mathrm{help}.. \\ $$
Answered by Dwaipayan Shikari last updated on 13/Sep/20
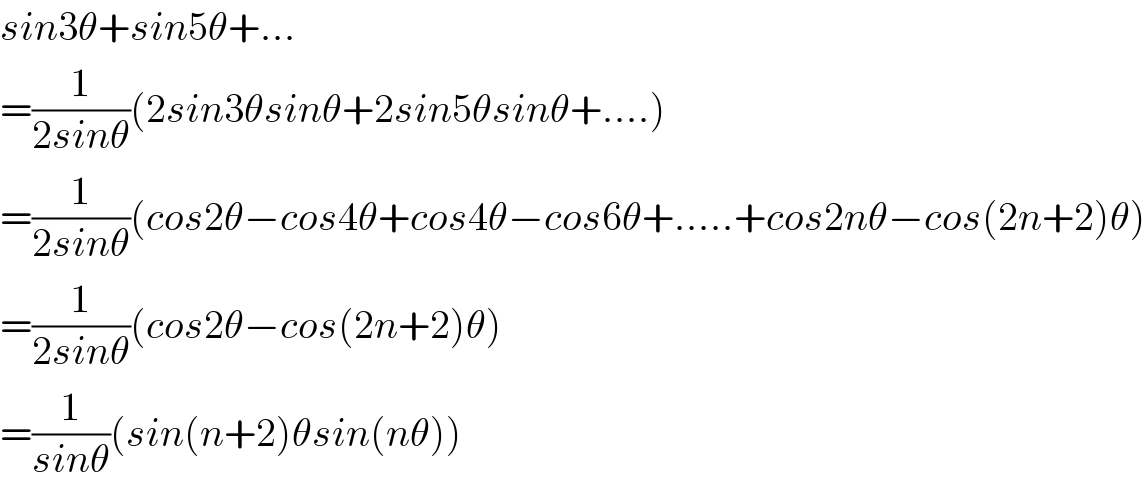
$${sin}\mathrm{3}\theta+{sin}\mathrm{5}\theta+… \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{sin}\theta}\left(\mathrm{2}{sin}\mathrm{3}\theta{sin}\theta+\mathrm{2}{sin}\mathrm{5}\theta{sin}\theta+….\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{sin}\theta}\left({cos}\mathrm{2}\theta−{cos}\mathrm{4}\theta+{cos}\mathrm{4}\theta−{cos}\mathrm{6}\theta+…..+{cos}\mathrm{2}{n}\theta−{cos}\left(\mathrm{2}{n}+\mathrm{2}\right)\theta\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{sin}\theta}\left({cos}\mathrm{2}\theta−{cos}\left(\mathrm{2}{n}+\mathrm{2}\right)\theta\right) \\ $$$$=\frac{\mathrm{1}}{{sin}\theta}\left({sin}\left({n}+\mathrm{2}\right)\theta{sin}\left({n}\theta\right)\right) \\ $$
Commented by ZiYangLee last updated on 14/Sep/20

$$\mathrm{Tks}! \\ $$
