Question Number 113452 by mathdave last updated on 13/Sep/20

Answered by maths mind last updated on 13/Sep/20
![x=sin(t) ⇒=∫_0 ^(π/2) ((tcos(t)dt)/(sin(t)+cos(t)))=I J=∫_0 ^(π/2) ((tsin(t))/(sin(t)+cos(t)))dt I+J=∫_0 ^(π/2) tdt=(π^2 /8) I−J=∫_0 ^(π/2) t((cos(t)−sin(t))/(sin(t)+cos(t)))dt IBP =[tln(sin(t)+cos(t))]_0 ^(π/2) −∫_0 ^(π/2) ln(sin(t)+cos(t))dt =−∫_0 ^(π/2) ln((√(2c))os((π/4)−t))dt =−∫_0 ^(π/2) ln((√2))dt−∫_0 ^(π/4) ln(cos((π/4)−t))dt−∫_(π/4) ^(π/2) ln(cos((π/4)−t))dt =−(π/4)ln(2)−∫_0 ^(π/4) cos(t)dt+∫_0 ^(π/4) cos((π/4)−(u+(π/4)))du =−(π/4)ln(2)−2∫_0 ^(π/4) ln(cos(t))dt lets find ∫_0 ^(π/4) ln(cos(t))dt_(=A) we use G=−∫_0 ^(π/4) ln(tg(t))dt=catalan Constante and call B=∫_0 ^(π/4) ln(sin(t))dt A−B=G A+B=∫_0 ^(π/4) ln(sin(2t)/2)dt=−ln(2)(π/4)+(1/2)∫_0 ^(π/2) ln(sin(x))dx =((−ln(2)π)/4)+(1/2).−((πlog(2))/2)=−((πlog(2))/2) A=(1/2)(G−π((log(2))/2)) I−J=−((πln(2))/4)−2.(1/2)(G−πlog(2).(1/2)) =−G+((πlog(2))/4) I=(1/2)(−G+((πlog(2))/4)+(π^2 /8))=∫_0 ^1 ((sin^(−1) (x))/(x+(√(1−x^2 ))))dx⋍0.431](https://www.tinkutara.com/question/Q113538.png)
$${x}={sin}\left({t}\right) \\ $$$$\Rightarrow=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{tcos}\left({t}\right){dt}}{{sin}\left({t}\right)+{cos}\left({t}\right)}={I} \\ $$$${J}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{tsin}\left({t}\right)}{{sin}\left({t}\right)+{cos}\left({t}\right)}{dt} \\ $$$${I}+{J}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {tdt}=\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$${I}−{J}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {t}\frac{{cos}\left({t}\right)−{sin}\left({t}\right)}{{sin}\left({t}\right)+{cos}\left({t}\right)}{dt}\:{IBP} \\ $$$$=\left[{tln}\left({sin}\left({t}\right)+{cos}\left({t}\right)\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} −\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({sin}\left({t}\right)+{cos}\left({t}\right)\right){dt} \\ $$$$=−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\sqrt{\mathrm{2}{c}}{os}\left(\frac{\pi}{\mathrm{4}}−{t}\right)\right){dt} \\ $$$$=−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\sqrt{\mathrm{2}}\right){dt}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\left(\frac{\pi}{\mathrm{4}}−{t}\right)\right){dt}−\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({cos}\left(\frac{\pi}{\mathrm{4}}−{t}\right)\right){dt} \\ $$$$=−\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {cos}\left({t}\right){dt}+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {cos}\left(\frac{\pi}{\mathrm{4}}−\left({u}+\frac{\pi}{\mathrm{4}}\right)\right){du} \\ $$$$=−\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\left({t}\right)\right){dt} \\ $$$${lets}\:{find}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\left({t}\right)\right){d}\underset{={A}} {{t}} \\ $$$${we}\:{use}\:{G}=−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({tg}\left({t}\right)\right){dt}={catalan}\:{Constante} \\ $$$${and}\:{call}\:{B}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({sin}\left({t}\right)\right){dt} \\ $$$${A}−{B}={G} \\ $$$${A}+{B}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({sin}\left(\mathrm{2}{t}\right)/\mathrm{2}\right){dt}=−{ln}\left(\mathrm{2}\right)\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({sin}\left({x}\right)\right){dx} \\ $$$$=\frac{−{ln}\left(\mathrm{2}\right)\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}.−\frac{\pi{log}\left(\mathrm{2}\right)}{\mathrm{2}}=−\frac{\pi{log}\left(\mathrm{2}\right)}{\mathrm{2}} \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{2}}\left({G}−\pi\frac{{log}\left(\mathrm{2}\right)}{\mathrm{2}}\right) \\ $$$${I}−{J}=−\frac{\pi{ln}\left(\mathrm{2}\right)}{\mathrm{4}}−\mathrm{2}.\frac{\mathrm{1}}{\mathrm{2}}\left({G}−\pi{log}\left(\mathrm{2}\right).\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=−{G}+\frac{\pi{log}\left(\mathrm{2}\right)}{\mathrm{4}} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\left(−{G}+\frac{\pi{log}\left(\mathrm{2}\right)}{\mathrm{4}}+\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{sin}^{−\mathrm{1}} \left({x}\right)}{{x}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}\backsimeq\mathrm{0}.\mathrm{431} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mathdave last updated on 14/Sep/20
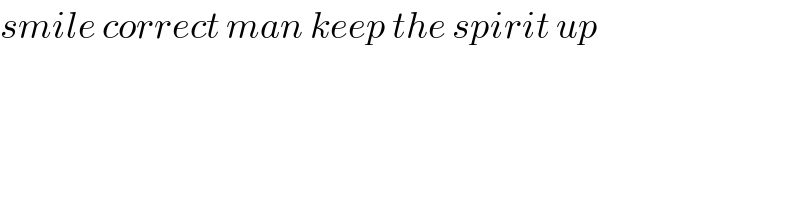
$${smile}\:{correct}\:{man}\:{keep}\:{the}\:{spirit}\:{up} \\ $$
Commented by Tawa11 last updated on 06/Sep/21

$$\mathrm{great}\:\mathrm{sir} \\ $$
