Question Number 113465 by Algoritm last updated on 13/Sep/20

Commented by Her_Majesty last updated on 13/Sep/20

$${use}\:{your}\:{brains} \\ $$$$\sqrt{\mathrm{2019}}\approx\mathrm{45} \\ $$$${how}\:{could}\:\mathrm{45}\left(\frac{\mathrm{1}}{\mathrm{45}+\mathrm{2019}}+\frac{\mathrm{1}}{\mathrm{45}+\mathrm{2019}^{\mathrm{2}} }+…\right) \\ $$$${be}\:{greater}\:{than}\:\mathrm{1}??? \\ $$$${if}\:{you}\:{start}\:{to}\:{try}\:{with} \\ $$$$\sqrt{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}+\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} +\sqrt{\mathrm{2}}}\right)\:{and}\:\sqrt{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{3}+\sqrt{\mathrm{3}}}+…+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3}} +\sqrt{\mathrm{3}}}\right) \\ $$$${and}\:\sqrt{\mathrm{4}}\left(\frac{\mathrm{1}}{\mathrm{4}+\sqrt{\mathrm{4}}}+…+\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{4}} +\sqrt{\mathrm{4}}}\right)\:{you}\:{might}\:{see} \\ $$$${that}\:\sqrt{{n}}\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{n}^{{i}} +\sqrt{{n}}}\:{can}\:{only}\:{be}\:{a}\:{rational} \\ $$$${number}\:{when}\:\sqrt{{n}}\:{is}\:{a}\:{rational}\:{number}. \\ $$$${also}\:{it}\:{can}\:{never}\:{be}\:{a}\sqrt{{n}}\:{with}\:{a}\in\mathbb{N} \\ $$
Commented by Algoritm last updated on 13/Sep/20

$$\mathrm{no}\:\mathrm{correct} \\ $$
Commented by Her_Majesty last updated on 13/Sep/20
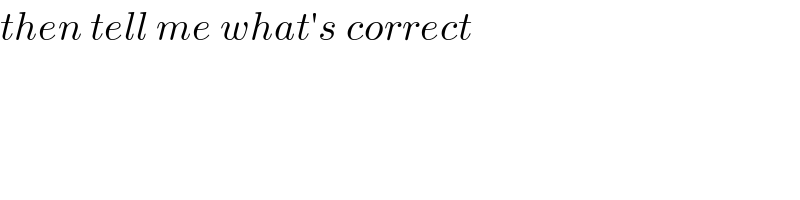
$${then}\:{tell}\:{me}\:{what}'{s}\:{correct} \\ $$
Commented by mr W last updated on 13/Sep/20
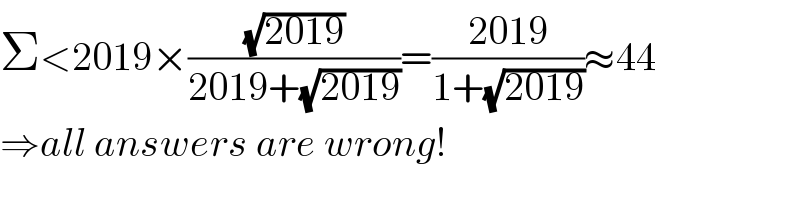
$$\Sigma<\mathrm{2019}×\frac{\sqrt{\mathrm{2019}}}{\mathrm{2019}+\sqrt{\mathrm{2019}}}=\frac{\mathrm{2019}}{\mathrm{1}+\sqrt{\mathrm{2019}}}\approx\mathrm{44} \\ $$$$\Rightarrow{all}\:{answers}\:{are}\:{wrong}! \\ $$
Commented by mr W last updated on 13/Sep/20
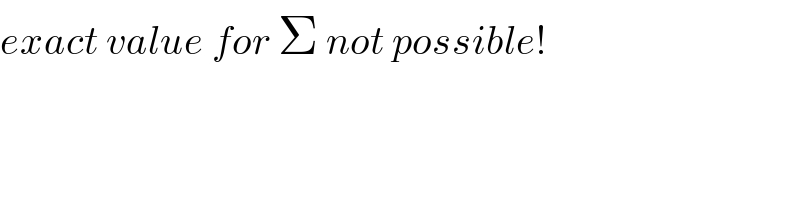
$${exact}\:{value}\:{for}\:\Sigma\:{not}\:{possible}! \\ $$
Commented by Algoritm last updated on 13/Sep/20

$$\mathrm{answer}\:\:? \\ $$
Commented by mr W last updated on 13/Sep/20

$${the}\:{answer}\:{is}\:{that}\:{the}\:{question}\:{is} \\ $$$${wrong}!\:{if}\:{you}\:{have}\:{a}\:{better}\:{answer}, \\ $$$${then}\:{tell}\:{us}! \\ $$
