Question-113505

Question Number 113505 by Lekhraj last updated on 13/Sep/20

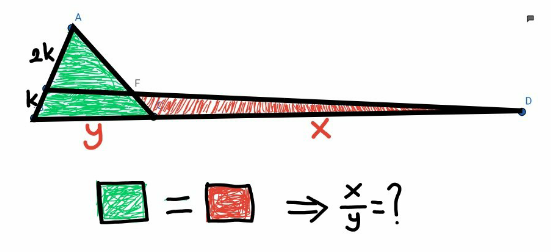
Answered by mr W last updated on 13/Sep/20

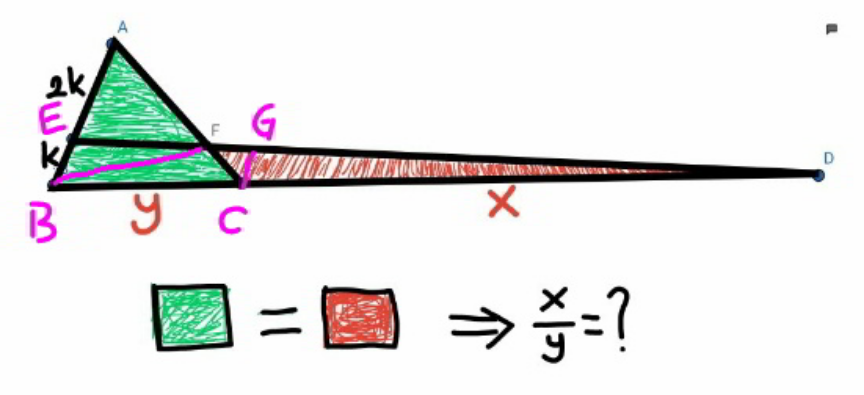
Commented by mr W last updated on 13/Sep/20

let λ=(y/x) ((CG)/(BE))=(x/(x+y))=(1/(1+(y/x)))=(1/(1+λ)) CG=(k/(1+λ)) ((CF)/(AF))=((CG)/(AE))=(k/(2k(1+λ)))=(1/(2(1+λ))) ((CF)/(CA))=((CF)/(CF+AF))=(1/(1+((AF)/(CF))))=(1/(1+2(1+λ)))=(1/(3+2λ)) ((ΔBCF)/(ΔBCA))=((CF)/(CA))=(1/(3+2λ)) ((ΔBCF)/(ΔCDF))=(y/x)=λ ((green)/(red))=((ΔBCA)/(ΔCDF))=((ΔBCA)/(ΔBCF))×((ΔBCF)/(ΔCDF))=1 ⇒(3+2λ)λ=1 ⇒2λ^2 +3λ−1=0 ⇒λ=(((√(17))−3)/4)=(y/x) ⇒(x/y)=(4/( (√(17))−3))=(((√(17))+3)/2)≈3.562

$${let}\:\lambda=\frac{{y}}{{x}} \\ $$$$\frac{{CG}}{{BE}}=\frac{{x}}{{x}+{y}}=\frac{\mathrm{1}}{\mathrm{1}+\frac{{y}}{{x}}}=\frac{\mathrm{1}}{\mathrm{1}+\lambda} \\ $$$${CG}=\frac{{k}}{\mathrm{1}+\lambda} \\ $$$$\frac{{CF}}{{AF}}=\frac{{CG}}{{AE}}=\frac{{k}}{\mathrm{2}{k}\left(\mathrm{1}+\lambda\right)}=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\lambda\right)} \\ $$$$\frac{{CF}}{{CA}}=\frac{{CF}}{{CF}+{AF}}=\frac{\mathrm{1}}{\mathrm{1}+\frac{{AF}}{{CF}}}=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}\left(\mathrm{1}+\lambda\right)}=\frac{\mathrm{1}}{\mathrm{3}+\mathrm{2}\lambda} \\ $$$$\frac{\Delta{BCF}}{\Delta{BCA}}=\frac{{CF}}{{CA}}=\frac{\mathrm{1}}{\mathrm{3}+\mathrm{2}\lambda} \\ $$$$\frac{\Delta{BCF}}{\Delta{CDF}}=\frac{{y}}{{x}}=\lambda \\ $$$$\frac{{green}}{{red}}=\frac{\Delta{BCA}}{\Delta{CDF}}=\frac{\Delta{BCA}}{\Delta{BCF}}×\frac{\Delta{BCF}}{\Delta{CDF}}=\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{3}+\mathrm{2}\lambda\right)\lambda=\mathrm{1} \\ $$$$\Rightarrow\mathrm{2}\lambda^{\mathrm{2}} +\mathrm{3}\lambda−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\lambda=\frac{\sqrt{\mathrm{17}}−\mathrm{3}}{\mathrm{4}}=\frac{{y}}{{x}} \\ $$$$\Rightarrow\frac{{x}}{{y}}=\frac{\mathrm{4}}{\:\sqrt{\mathrm{17}}−\mathrm{3}}=\frac{\sqrt{\mathrm{17}}+\mathrm{3}}{\mathrm{2}}\approx\mathrm{3}.\mathrm{562} \\ $$

Commented by Lekhraj last updated on 14/Sep/20

Thanks a lot sir for such a nice and great solution . Have you any twitter handle sir I like to follow you .

$${T}\mathrm{hanks}\:\mathrm{a}\:\mathrm{lot}\:\mathrm{sir}\:\mathrm{for}\:\mathrm{such}\:\mathrm{a}\:\mathrm{nice}\:\mathrm{and} \\ $$$$\mathrm{great}\:\mathrm{solution}\:.\:\mathrm{Have}\:\mathrm{you}\:\mathrm{any}\: \\ $$$$\mathrm{twitter}\:\mathrm{handle}\:\mathrm{sir}\:\mathrm{I}\:{like}\:{to}\:{follow}\: \\ $$$${you}\:.\: \\ $$

Commented by mr W last updated on 14/Sep/20

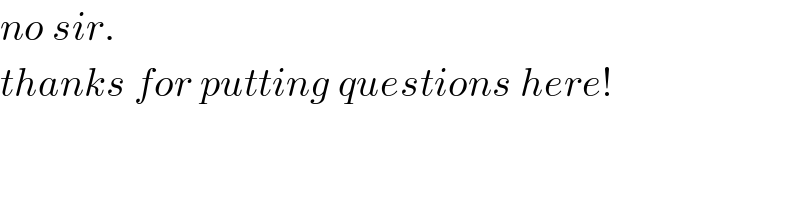
$${no}\:{sir}. \\ $$$${thanks}\:{for}\:{putting}\:{questions}\:{here}! \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply