Question-113507

Question Number 113507 by Khalmohmmad last updated on 13/Sep/20

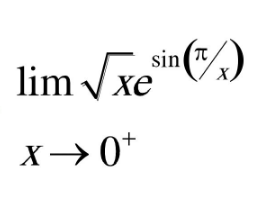
Answered by Dwaipayan Shikari last updated on 13/Sep/20

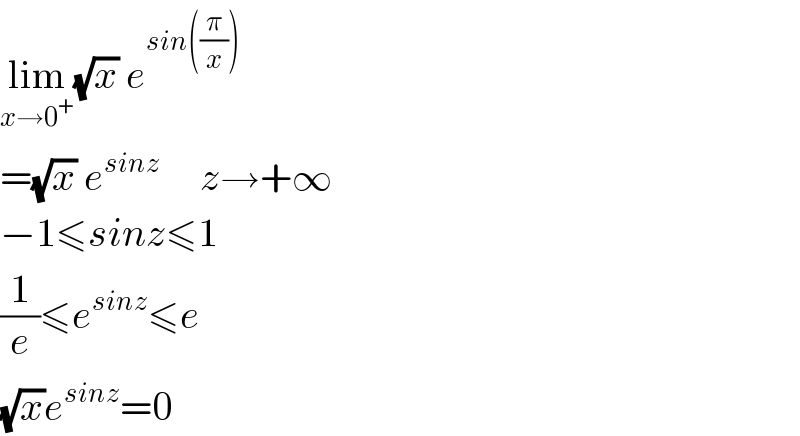
lim_(x→0^+ ) (√x) e^(sin((π/x))) =(√x) e^(sinz) z→+∞ −1≤sinz≤1 (1/e)≤e^(sinz) ≤e (√x)e^(sinz) =0

$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\sqrt{{x}}\:{e}^{{sin}\left(\frac{\pi}{{x}}\right)} \\ $$$$=\sqrt{{x}}\:{e}^{{sinz}} \:\:\:\:\:{z}\rightarrow+\infty \\ $$$$−\mathrm{1}\leqslant{sinz}\leqslant\mathrm{1} \\ $$$$\frac{\mathrm{1}}{{e}}\leqslant{e}^{{sinz}} \leqslant{e} \\ $$$$\sqrt{{x}}{e}^{{sinz}} =\mathrm{0} \\ $$

Answered by mathmax by abdo last updated on 13/Sep/20

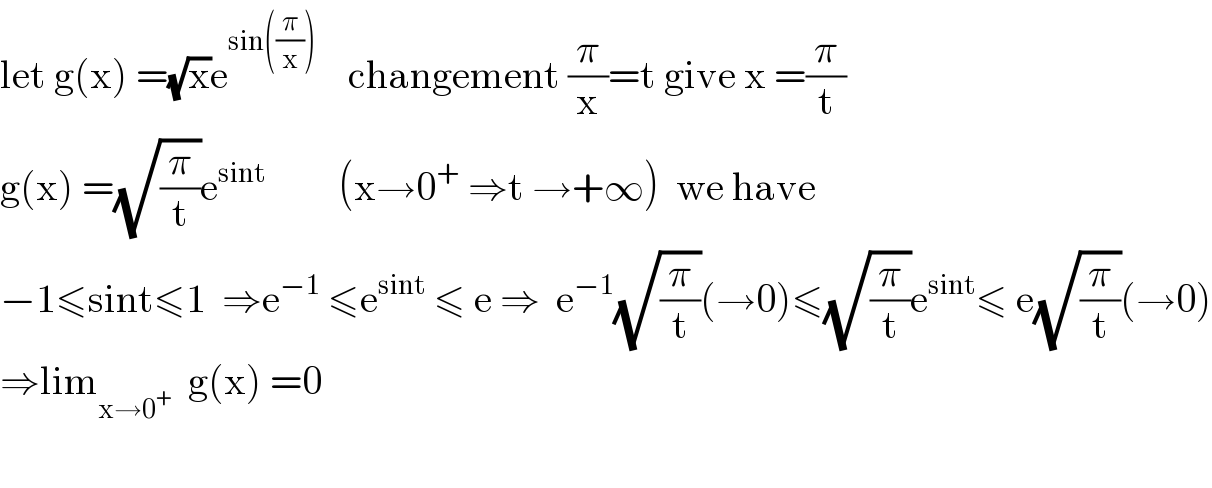
let g(x) =(√x)e^(sin((π/x))) changement (π/x)=t give x =(π/t) g(x) =(√(π/t))e^(sint) (x→0^+ ⇒t →+∞) we have −1≤sint≤1 ⇒e^(−1) ≤e^(sint) ≤ e ⇒ e^(−1) (√(π/t))(→0)≤(√(π/t))e^(sint) ≤ e(√(π/t))(→0) ⇒lim_(x→0^+ ) g(x) =0

$$\mathrm{let}\:\mathrm{g}\left(\mathrm{x}\right)\:=\sqrt{\mathrm{x}}\mathrm{e}^{\mathrm{sin}\left(\frac{\pi}{\mathrm{x}}\right)} \:\:\:\:\mathrm{changement}\:\frac{\pi}{\mathrm{x}}=\mathrm{t}\:\mathrm{give}\:\mathrm{x}\:=\frac{\pi}{\mathrm{t}} \\ $$$$\mathrm{g}\left(\mathrm{x}\right)\:=\sqrt{\frac{\pi}{\mathrm{t}}}\mathrm{e}^{\mathrm{sint}} \:\:\:\:\:\:\:\:\:\left(\mathrm{x}\rightarrow\mathrm{0}^{+} \:\Rightarrow\mathrm{t}\:\rightarrow+\infty\right)\:\:\mathrm{we}\:\mathrm{have} \\ $$$$−\mathrm{1}\leqslant\mathrm{sint}\leqslant\mathrm{1}\:\:\Rightarrow\mathrm{e}^{−\mathrm{1}} \:\leqslant\mathrm{e}^{\mathrm{sint}} \:\leqslant\:\mathrm{e}\:\Rightarrow\:\:\mathrm{e}^{−\mathrm{1}} \sqrt{\frac{\pi}{\mathrm{t}}}\left(\rightarrow\mathrm{0}\right)\leqslant\sqrt{\frac{\pi}{\mathrm{t}}}\mathrm{e}^{\mathrm{sint}} \leqslant\:\mathrm{e}\sqrt{\frac{\pi}{\mathrm{t}}}\left(\rightarrow\mathrm{0}\right) \\ $$$$\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}^{+} } \:\:\mathrm{g}\left(\mathrm{x}\right)\:=\mathrm{0} \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply