Question-113508

Facebook Tweet Pin

Question Number 113508 by Lekhraj last updated on 13/Sep/20

Commented by mr W last updated on 13/Sep/20

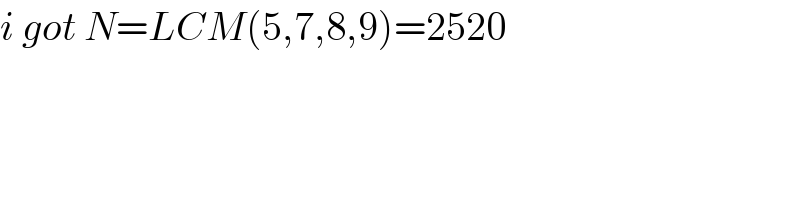
$${i}\:{got}\:{N}={LCM}\left(\mathrm{5},\mathrm{7},\mathrm{8},\mathrm{9}\right)=\mathrm{2520} \\ $$

Commented by Rasheed.Sindhi last updated on 13/Sep/20

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{N}=\mathrm{252} \\ $$

Answered by Rasheed.Sindhi last updated on 13/Sep/20

10N+1≡0(mod 1) No restriction on N 10N+2≡0(mod 2) No restriction on N 10N+3≡0(mod 3) ⇒3 ∣ N 10N+4≡0(mod 4) ⇒2 ∣ N 10N+5≡0(mod 5) No restriction on N 10N+6≡0(mod 6) ⇒3 ∣ N 10N+7≡0(mod 7) ⇒7 ∣ N 10N+8≡0(mod 8) ⇒4 ∣ N 10N+9≡0(mod 9) ⇒9 ∣ N Hence N is the least number which is divisible by 2,3,4,7 & 9 N=LCM(2,3,4,7,9) =LCM(4,7,9)=252

$$\mathrm{10N}+\mathrm{1}\equiv\mathrm{0}\left({mod}\:\mathrm{1}\right) \\ $$$${No}\:{restriction}\:{on}\:\mathrm{N} \\ $$$$\mathrm{10N}+\mathrm{2}\equiv\mathrm{0}\left({mod}\:\mathrm{2}\right) \\ $$$${No}\:{restriction}\:{on}\:\mathrm{N} \\ $$$$\mathrm{10N}+\mathrm{3}\equiv\mathrm{0}\left({mod}\:\mathrm{3}\right) \\ $$$$\Rightarrow\mathrm{3}\:\mid\:\mathrm{N} \\ $$$$\mathrm{10N}+\mathrm{4}\equiv\mathrm{0}\left({mod}\:\mathrm{4}\right) \\ $$$$\:\Rightarrow\mathrm{2}\:\mid\:\mathrm{N} \\ $$$$\mathrm{10N}+\mathrm{5}\equiv\mathrm{0}\left({mod}\:\mathrm{5}\right) \\ $$$${No}\:{restriction}\:{on}\:\mathrm{N} \\ $$$$\mathrm{10N}+\mathrm{6}\equiv\mathrm{0}\left({mod}\:\mathrm{6}\right) \\ $$$$\Rightarrow\mathrm{3}\:\mid\:\mathrm{N} \\ $$$$\mathrm{10N}+\mathrm{7}\equiv\mathrm{0}\left({mod}\:\mathrm{7}\right) \\ $$$$\Rightarrow\mathrm{7}\:\mid\:\mathrm{N} \\ $$$$\mathrm{10N}+\mathrm{8}\equiv\mathrm{0}\left({mod}\:\mathrm{8}\right) \\ $$$$\Rightarrow\mathrm{4}\:\mid\:\mathrm{N} \\ $$$$\mathrm{10N}+\mathrm{9}\equiv\mathrm{0}\left({mod}\:\mathrm{9}\right) \\ $$$$\Rightarrow\mathrm{9}\:\mid\:\mathrm{N}\: \\ $$$${Hence}\:{N}\:{is}\:{the}\:{least}\:{number} \\ $$$${which}\:{is}\:{divisible}\:{by}\:\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{7}\:\&\:\mathrm{9} \\ $$$$\mathrm{N}=\mathrm{LCM}\left(\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{7},\mathrm{9}\right) \\ $$$$\:\:\:\:\:=\mathrm{LCM}\left(\mathrm{4},\mathrm{7},\mathrm{9}\right)=\mathrm{252} \\ $$

Commented by mr W last updated on 13/Sep/20