Question Number 113510 by Lekhraj last updated on 13/Sep/20
Answered by MJS_new last updated on 13/Sep/20
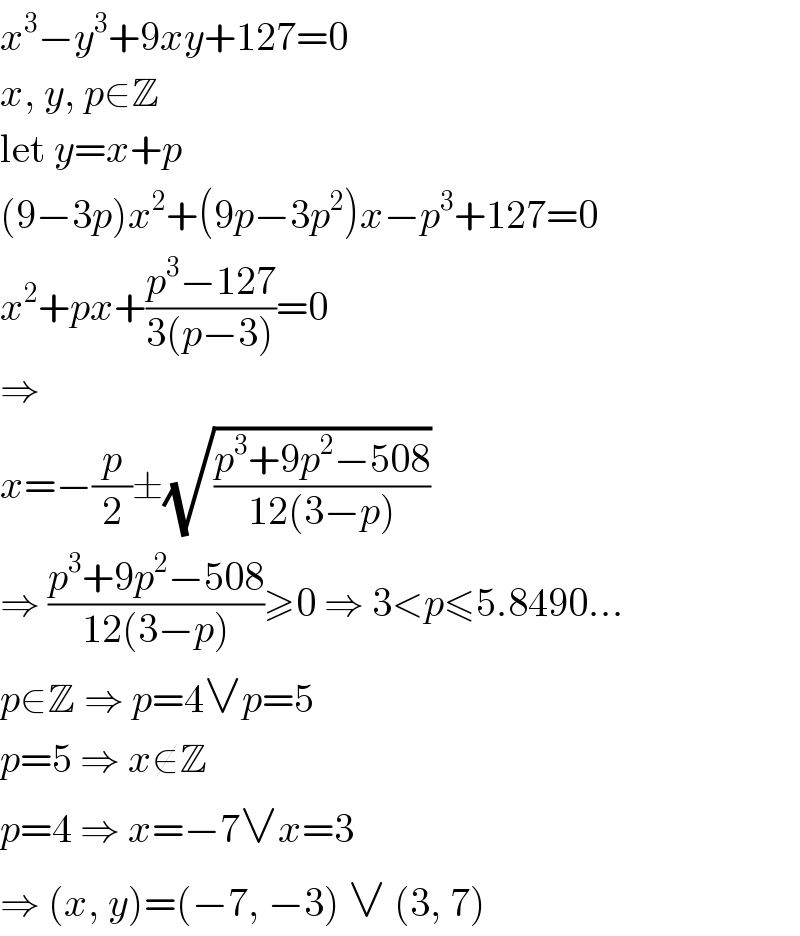
$${x}^{\mathrm{3}} −{y}^{\mathrm{3}} +\mathrm{9}{xy}+\mathrm{127}=\mathrm{0} \\ $$$${x},\:{y},\:{p}\in\mathbb{Z} \\ $$$$\mathrm{let}\:{y}={x}+{p} \\ $$$$\left(\mathrm{9}−\mathrm{3}{p}\right){x}^{\mathrm{2}} +\left(\mathrm{9}{p}−\mathrm{3}{p}^{\mathrm{2}} \right){x}−{p}^{\mathrm{3}} +\mathrm{127}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} +{px}+\frac{{p}^{\mathrm{3}} −\mathrm{127}}{\mathrm{3}\left({p}−\mathrm{3}\right)}=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${x}=−\frac{{p}}{\mathrm{2}}\pm\sqrt{\frac{{p}^{\mathrm{3}} +\mathrm{9}{p}^{\mathrm{2}} −\mathrm{508}}{\mathrm{12}\left(\mathrm{3}−{p}\right)}} \\ $$$$\Rightarrow\:\frac{{p}^{\mathrm{3}} +\mathrm{9}{p}^{\mathrm{2}} −\mathrm{508}}{\mathrm{12}\left(\mathrm{3}−{p}\right)}\geqslant\mathrm{0}\:\Rightarrow\:\mathrm{3}<{p}\leqslant\mathrm{5}.\mathrm{8490}… \\ $$$${p}\in\mathbb{Z}\:\Rightarrow\:{p}=\mathrm{4}\vee{p}=\mathrm{5} \\ $$$${p}=\mathrm{5}\:\Rightarrow\:{x}\notin\mathbb{Z} \\ $$$${p}=\mathrm{4}\:\Rightarrow\:{x}=−\mathrm{7}\vee{x}=\mathrm{3} \\ $$$$\Rightarrow\:\left({x},\:{y}\right)=\left(−\mathrm{7},\:−\mathrm{3}\right)\:\vee\:\left(\mathrm{3},\:\mathrm{7}\right) \\ $$
Commented by Lekhraj last updated on 14/Sep/20

$${T}\mathrm{hanks} \\ $$
