Question Number 113511 by Khalmohmmad last updated on 13/Sep/20
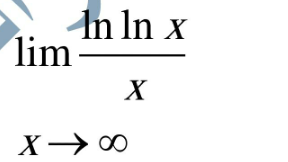
Answered by mathmax by abdo last updated on 13/Sep/20
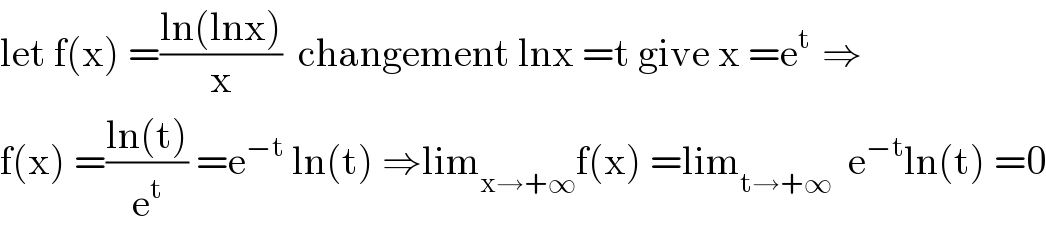
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{ln}\left(\mathrm{lnx}\right)}{\mathrm{x}}\:\:\mathrm{changement}\:\mathrm{lnx}\:=\mathrm{t}\:\mathrm{give}\:\mathrm{x}\:=\mathrm{e}^{\mathrm{t}\:} \:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{ln}\left(\mathrm{t}\right)}{\mathrm{e}^{\mathrm{t}} }\:=\mathrm{e}^{−\mathrm{t}} \:\mathrm{ln}\left(\mathrm{t}\right)\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{lim}_{\mathrm{t}\rightarrow+\infty} \:\:\mathrm{e}^{−\mathrm{t}} \mathrm{ln}\left(\mathrm{t}\right)\:=\mathrm{0} \\ $$
