Menu Close

Question-113675

Tinku Tara 0 Comments
Pin




Question Number 113675 by AbhishekBasnet last updated on 14/Sep/20
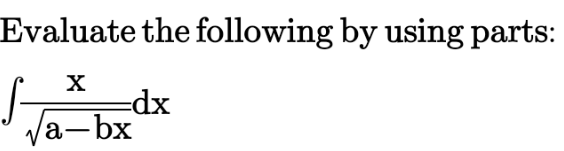
Commented by mohammad17 last updated on 14/Sep/20
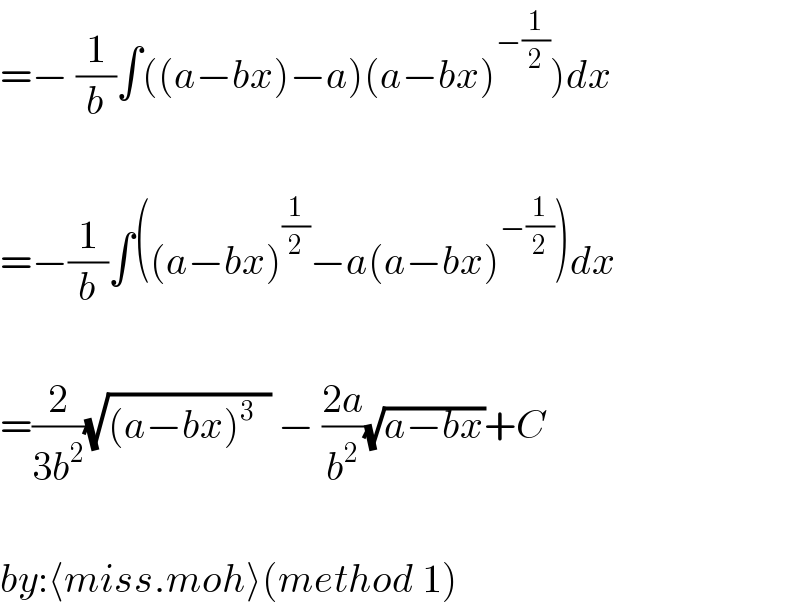
=− (1/b)∫((a−bx)−a)(a−bx)^(−(1/2)) )dx =−(1/b)∫((a−bx)^(1/2) −a(a−bx)^(−(1/2)) )dx =(2/(3b^2 ))(√((a−bx)^3 )) − ((2a)/b^2 )(√(a−bx))+C by:⟨miss.moh⟩(method 1)
$$\left.=−\:\frac{\mathrm{1}}{{b}}\int\left(\left({a}−{bx}\right)−{a}\right)\left({a}−{bx}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \right){dx} \\ $$$$ \\ $$$$=−\frac{\mathrm{1}}{{b}}\int\left(\left({a}−{bx}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} −{a}\left({a}−{bx}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \right){dx} \\ $$$$ \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}{b}^{\mathrm{2}} }\sqrt{\left({a}−{bx}\right)^{\mathrm{3}} \:\:}\:−\:\frac{\mathrm{2}{a}}{{b}^{\mathrm{2}} }\sqrt{{a}−{bx}}+{C} \\ $$$$ \\ $$$${by}:\langle{miss}.{moh}\rangle\left({method}\:\mathrm{1}\right) \\ $$
Commented by mohammad17 last updated on 14/Sep/20
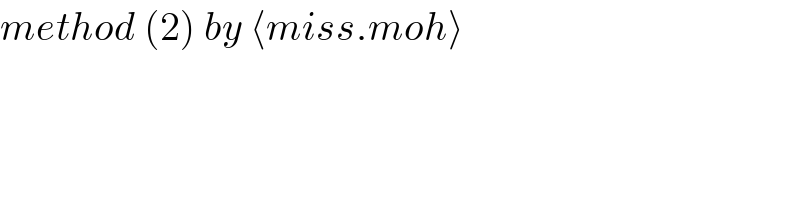
method (2) by ⟨miss.moh⟩
$${method}\:\left(\mathrm{2}\right)\:{by}\:\langle{miss}.{moh}\rangle \\ $$
Commented by mohammad17 last updated on 14/Sep/20
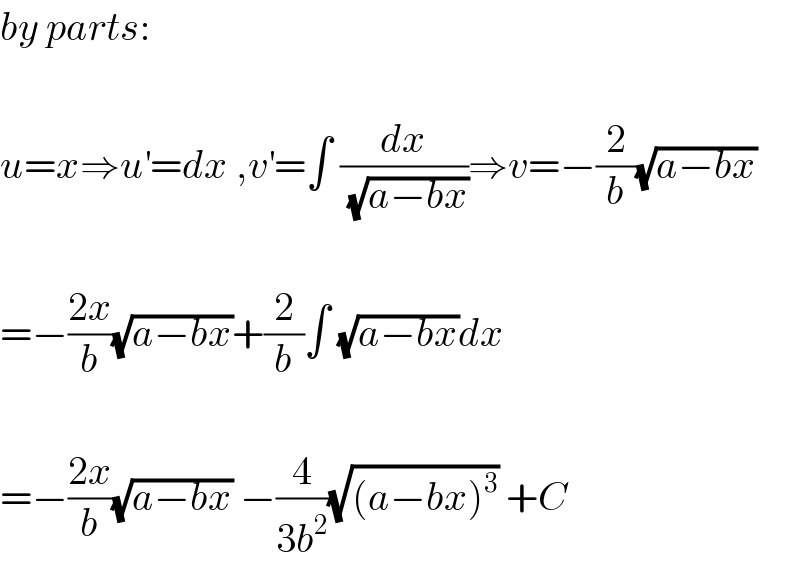
by parts: u=x⇒u^′ =dx ,v^′ =∫ (dx/( (√(a−bx))))⇒v=−(2/b)(√(a−bx)) =−((2x)/b)(√(a−bx))+(2/b)∫ (√(a−bx))dx =−((2x)/b)(√(a−bx)) −(4/(3b^2 ))(√((a−bx)^3 )) +C
$${by}\:{parts}: \\ $$$$ \\ $$$${u}={x}\Rightarrow{u}^{'} ={dx}\:,{v}^{'} =\int\:\frac{{dx}}{\:\sqrt{{a}−{bx}}}\Rightarrow{v}=−\frac{\mathrm{2}}{{b}}\sqrt{{a}−{bx}} \\ $$$$ \\ $$$$=−\frac{\mathrm{2}{x}}{{b}}\sqrt{{a}−{bx}}+\frac{\mathrm{2}}{{b}}\int\:\sqrt{{a}−{bx}}{dx} \\ $$$$ \\ $$$$=−\frac{\mathrm{2}{x}}{{b}}\sqrt{{a}−{bx}}\:−\frac{\mathrm{4}}{\mathrm{3}{b}^{\mathrm{2}} }\sqrt{\left({a}−{bx}\right)^{\mathrm{3}} }\:+{C} \\ $$
Answered by Dwaipayan Shikari last updated on 14/Sep/20
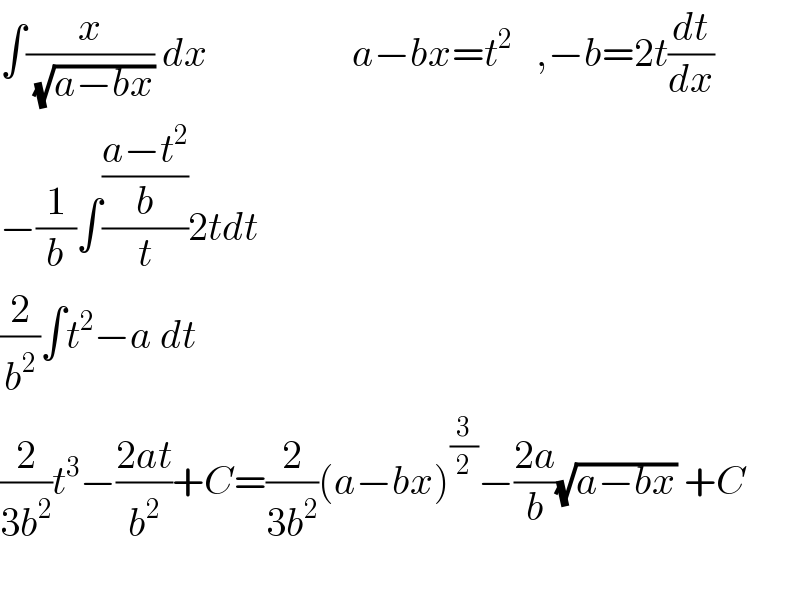
∫(x/( (√(a−bx)))) dx a−bx=t^2 ,−b=2t(dt/dx) −(1/b)∫(((a−t^2 )/b)/t)2tdt (2/b^2 )∫t^2 −a dt (2/(3b^2 ))t^3 −((2at)/b^2 )+C=(2/(3b^2 ))(a−bx)^(3/2) −((2a)/b)(√(a−bx)) +C
$$\int\frac{{x}}{\:\sqrt{{a}−{bx}}}\:{dx}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}−{bx}={t}^{\mathrm{2}} \:\:\:,−{b}=\mathrm{2}{t}\frac{{dt}}{{dx}} \\ $$$$−\frac{\mathrm{1}}{{b}}\int\frac{\frac{{a}−{t}^{\mathrm{2}} }{{b}}}{{t}}\mathrm{2}{tdt} \\ $$$$\frac{\mathrm{2}}{{b}^{\mathrm{2}} }\int{t}^{\mathrm{2}} −{a}\:{dt}\:\:\:\: \\ $$$$\frac{\mathrm{2}}{\mathrm{3}{b}^{\mathrm{2}} }{t}^{\mathrm{3}} −\frac{\mathrm{2}{at}}{{b}^{\mathrm{2}} }+{C}=\frac{\mathrm{2}}{\mathrm{3}{b}^{\mathrm{2}} }\left({a}−{bx}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{2}{a}}{{b}}\sqrt{{a}−{bx}}\:+{C} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *